查看数据源：599165c92bfec200011e17b5
设函数 $f\left(x\right)=\left(x-1\right)^3-ax-b$，$x\in \mathbb R$，其中 $a,b\in \mathbb R$．
【难度】
【出处】
无
【标注】
  1. 求 $f\left(x\right)$ 的单调区间；
    标注
    答案
    当 $ a\leqslant 0 $ 时，函数 $ f\left(x\right) $ 的单调递增区间为 $ \left(-\infty,+\infty\right) $，没有单调递减区间．
    当 $ a>0 $ 时，函数 $ f\left(x\right) $ 的单调递增区间是 $ \left(-\infty,-\dfrac{\sqrt{3a}}3+1\right) $ 和 $ \left(\dfrac{\sqrt{3a}}3+1,+\infty\right) $，单调递减区间是 $ \left(-\dfrac{\sqrt{3a}}3+1,\dfrac{\sqrt{3a}}3+1\right) $．
    解析
    本题考查利用导数研究函数的单调性，需要分类讨论．函数 $ f\left(x\right) $ 的导函数 $ f'\left(x\right)=3\left(x-1\right)^2-a $．
    情形一：$ a\leqslant 0 $．
    此时恒有 $ f'\left(x\right)\geqslant 0 $，于是函数 $ f\left(x\right) $ 的单调递增区间为 $ \left(-\infty,+\infty\right) $，没有单调递减区间．
    情形二：$ a>0 $．
    此时函数 $ f'\left(x\right) $ 有两个零点，函数 $ f\left(x\right) $ 的单调递增区间是 $ \left(-\infty,-\dfrac{\sqrt{3a}}3+1\right) $ 和 $ \left(\dfrac{\sqrt{3a}}3+1,+\infty\right) $，单调递减区间是 $ \left(-\dfrac{\sqrt{3a}}3+1,\dfrac{\sqrt{3a}}3+1\right) $．
  2. 若 $f\left(x\right)$ 存在极值点 $x_0$，且 $f\left(x_1\right)=f\left(x_0\right)$，其中 $x_1\neq x_0$，求证：$x_1+2x_0=3$；
    标注
    答案
    略．
    解析
    注意要证结论即为 $ x_1=3-2x_0 $，而且可得到 $ f\left(3-2x_0\right)=f\left(x_0\right) $．因为 $ x_0 $ 是 $ f\left(x\right) $ 的极值点，故由第（1）问可知，$ a>0 $，且 $ f'\left(x_0\right)=0 $，即 $ a=3\left(x_0-1\right)^2 >0 $．由题意可知，关于 $ x $ 的方程 $ f\left(x\right)=f \left(x_0\right) $ 有且只有两个不同的实根 $ x_0,x_1 $．因为\[\begin{split}f \left(3-2x_0\right) &=\left(2-2x_0\right)^3-3\left(x_0-1\right)^2\left(3-2x_0\right)-b\\&=\left(x_0-1\right)^2\cdot\left(-2x_0-1\right)-b\\&=\left(x_0-1\right)^3-3x_0\left(x_0-1\right)^2-b\\&=\left(x_0-1\right)^3-ax_0-b\\&=f\left(x_0\right), \end{split} \]且 $ 3-2x_0\ne x_0 $（否则由 $ x_0=1 $ 可推出 $ a=0 $，矛盾），故\[ 3-2x_0=x_1, 即 x_1+2x_0=3. \]
  3. 设 $a>0$，函数 $g\left(x\right)=|f\left(x\right)|$，求证：$g\left(x\right)$ 在区间 $\left[0,2\right]$ 上的最大值不小于 $\dfrac 14$．
    标注
    答案
    略．
    解析
    可以在第二问的基础上，画出极端情形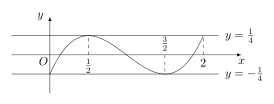：在此基础上利用函数 $f(x)$ 在 $ x=0,\dfrac 12,\dfrac 32,2 $ 处的函数值，结合反证法证明结论即可．用反证法．假设 $ g\left(x\right) $ 在区间 $ \left[0,2\right] $ 上的最大值小于 $ \dfrac 14 $．
    考虑\[ \begin{cases}f\left(0\right)=-1-b,\\f\left(2\right)=1-2a-b,\\f \left(\dfrac{3}{2} \right)=\dfrac{1}{8}-\dfrac{3}{2}a-b,\\f \left(\dfrac{1}{2} \right)=-\dfrac{1}{8}-\dfrac{1}{2}a-b, \end{cases} \]我们有\[ \begin{cases}2-2a=f\left(2\right)-f\left(0\right),\\a- \dfrac{1}{4}=f \left(\dfrac{1}{2} \right)-f \left(\dfrac{3}{2} \right), \end{cases} \]所以\[ 2f \left(\dfrac{1}{2} \right)-2f \left(\dfrac{3}{2} \right)+f\left(2\right)-f\left(0\right)=\dfrac{3}{2}, \]但是\[ \left|2f \left(\dfrac{1}{2} \right)-2f \left(\dfrac{3}{2} \right)+f\left(2\right)-f\left(0\right)\right|\leqslant 2\left|f\left(\dfrac{1}{2} \right) \right|+2\left|f\left(\dfrac{3}{2} \right) \right|+\left|f\left(2 \right) \right|+\left|f\left(0 \right) \right|<\dfrac{3}{2}, \]矛盾．
    所以 $ g\left(x\right) $ 在区间 $ \left[0,2\right] $ 上的最大值不小于 $ \dfrac 14 $．
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2 问题3 答案3 解析3 备注3
0.113553s