如图，在平面直角坐标系 $xOy$ 中，已知以 $M$ 为圆心的圆 $M:x^2+y^2-12x-14y+60=0$ 及其上一点 $A\left(2,4\right)$．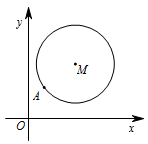
【难度】
【出处】
无
【标注】
-
设圆 $N$ 与 $x$ 轴相切，与圆 $M$ 外切，且圆心 $N$ 在直线 $x=6$ 上，求圆 $N$ 的标准方程；标注答案圆 $N$ 的标准方程为 ${{\left( x-6 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1$．解析考查圆的标准方程的求法，涉及直线与圆以及圆与圆的相切的知识．将圆 $ M $ 的方程整理为标准方程：$ \left(x-6\right)^2+\left(y-7\right)^2=25 $．
由于圆 $ M $ 与圆 $ N $ 的圆心连线与 $ x $ 轴垂直，于是圆 $ N $ 与 $ x $ 轴和圆 $ M $ 的切点分别是 $ \left(6,0\right) $和 $ \left(6,2\right) $，进而其标准方程为 $ \left(x-6\right)^2+\left(y-1\right)^2=1 $． -
设平行于 $OA$ 的直线 $l$ 与圆 $M$ 相交于 $B$，$C$ 两点，且 $BC=OA$，求直线 $l$ 的方程；标注答案$l$：$y=2x+5$ 或 $y=2x-15$．解析考查直线与圆的位置关系中的弦长问题．由题意得 $OA=2\sqrt{5}$，$ {{k}_{OA}}=2 $．
设 $l:y=2x+b$，则圆心 $M$ 到直线 $l$ 的距离为\[d=\dfrac{\left| 12-7+b \right|}{\sqrt{{{2}^{2}}+1}}=\dfrac{\left| 5+b \right|}{\sqrt{5}},\]则\[BC=2\sqrt{{{5}^{2}}-{{d}^{2}}}=2\sqrt{25-\dfrac{{{\left( 5+b \right)}^{2}}}{5}},\]又因为 $BC=2\sqrt{5}$，所以\[2\sqrt{25-\dfrac{{{\left( 5+b \right)}^{2}}}{5}}=2\sqrt{5},\]解得 $b=5$ 或 $b=-15$．
所以 $l$：$y=2x+5$ 或 $y=2x-15$． -
设点 $T\left(t,0\right)$ 满足：存在 圆 $M$ 上的两点 $P$ 和 $Q$，使得 $\overrightarrow {TA}+\overrightarrow {TP}=\overrightarrow {TQ}$，求实数 $t$ 的取值范围．标注答案实数 $t$ 的取值范围是 $ \left[ 2-2\sqrt{21},2+2\sqrt{21} \right]$．解析考查利用轨迹研究动态问题的数学思维．由题意，$\overrightarrow{AT}=\overrightarrow{TP}-\overrightarrow{TQ}=\overrightarrow{QP}$．而 $Q,P$ 可以在圆 $M$ 上任取，因此 $\overrightarrow{QP}$ 可以表示任何长度不超过圆 $M$ 的直径的向量．
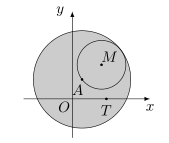于是问题等价于点 $T\left(t,0\right)$ 在圆 $A:\left(x-2\right)^2+\left(y-4\right)^2=100$ 的圆内部（包含边界），即\[\left(t-2\right)^2+\left(0-4\right)^2\leqslant 100,\]解得 $2-2\sqrt{21}\leqslant t\leqslant 2+2\sqrt{21}$，因此实数 $t$ 的取值范围是 $\left[2-2\sqrt{21},2+2\sqrt{21}\right]$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
