如图,设抛物线 $y^2=2px\left(p>0\right)$ 的焦点为 $F$,抛物线上的点 $A$ 到 $y$ 轴的距离等于 $|AF|-1$.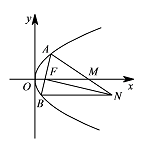

【难度】
【出处】
无
【标注】
-
求 $p$ 的值;标注答案$p=2$.解析本题考查抛物线的定义.由题意可得,抛物线上点 $A$ 到焦点 $F$ 的距离等于点 $A$ 到直线 $x=-1$ 的距离,由抛物线的定义得 $\dfrac p2=1$,即 $p=2$.
-
若直线 $AF$ 交抛物线于另一点 $B$,过 $B$ 与 $x$ 轴平行的直线和过 $F$ 与 $AB$ 垂直的直线交于点 $N$,$AN$ 与 $x$ 轴交于点 $M$.求 $M$ 的横坐标的取值范围.标注答案$\left(-\infty,0\right)\cup\left(2,+\infty\right)$.解析本题考查取值范围问题,先结合已知条件把 $M$ 点的横坐标表示出来,然后再求取值范围即可.由(I)得,抛物线的方程为 $y^2=4x$,$F\left(1,0\right)$,可设 $A\left(t^2,2t\right)$,$t\ne 0,t\ne \pm1$.
因为 $AF$ 不垂直于 $y$ 轴,可设直线 $AF:x=sy+1,\left(s\ne 0\right)$,由 $ \begin{cases}y^2=4x,\\x=sy+1\end{cases} $ 消去 $x$得\[y^2-4sy-4=0.\]故 $y_1y_2=-4$,所以 $B\left(\dfrac 1{t^2},-\dfrac 2t\right)$.
又直线 $AB$ 的斜率为 $\dfrac{2t}{t^2-1}$,故直线 $FN$ 的斜率为 $-\dfrac{t^2-1}{2t}$.
从而得直线 $FN:y=-\dfrac{t^2-1}{2t}\left(x-1\right)$,直线 $BN:y=-\dfrac 2t$.所以\[N\left(\dfrac{t^2+3}{t^2-1},-\dfrac 2t\right).\]设 $M\left(m,0\right)$,由 $A$,$M$,$N$ 三点共线得\[\dfrac{2t}{t^2-m}=\dfrac{2t+\frac 2t}{t^2-\frac{t^2+3}{t^2-1}},\]于是有\[m=\dfrac{2t^2}{t^2-1}.\]所以\[m<0 或 m>2.\]经检验,$m<0$ 或 $m>2$ 满足题意.
综上,点 $M$ 的横坐标的取值范围是 $\left(-\infty,0\right)\cup\left(2,+\infty\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2