如图,在三棱锥 $P-ABC$ 中,$PA\perp AB$,$PA\perp BC$,$AB\perp BC$,$PA=AB=BC=2$,$D$ 为线段 $AC$ 的中点,$E$ 为线段 $PC$ 上一点.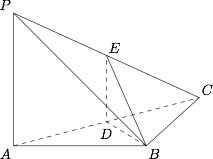

【难度】
【出处】
2017年高考北京卷(文)
【标注】
-
求证:$PA\perp BD$;标注答案略解析因为 $PA\perp AB$,$PA\perp BC$,$AB\cap BC=B$,所以$$PA\perp \text{平面}ABC.$$因为 $BD\subset $ 平面 $ABC$,所以$$PA\perp BD.$$
-
求证:平面 $BDE\perp$ 平面 $PAC$;标注答案略解析在 $\triangle{ABC}$ 中,因为 $AB=BC$,$D$ 为 $AC$ 中点,所以$$BD\perp AC.$$又 $PA\perp BD$,$AC\cap PA=A$,所以$$BD\perp {\text{平面}}PAC.$$又因为 $BD\subset $ 平面 $BDE$,所以$$\text{平面}BDE\perp \text{平面}PAC.$$
-
当 $PA\parallel$ 平面 $BDE$ 时,求三棱锥 $E-BCD$ 的体积.标注答案$\dfrac 13$解析因为 $PA\parallel $ 平面 $BDE$,$PA\subset$ 平面 $PAC$,且平面 $PAC\cap $ 平面 $BDE=DE$,所以$$PA\parallel DE.$$因为 $PA\parallel$ 平面 $ABC$,所以$$DE\perp \text{平面}ABC.$$所以 $DE$ 为三棱锥 $E-BCD$ 的高.
又因为 $D$ 为 $AC$ 中点,$E$ 为 $PC$ 中点,所以$$DE=\dfrac 12 PA=1 ,AC=\sqrt{AB^2+BC^2}=2\sqrt 2.$$在 $\triangle{ABC}$ 中,$DC=\dfrac 12 AC=\sqrt 2$.
因为 $BC=BA$,$\angle{ABC}=90^{\circ}$,所以$$DB=DC=\sqrt 2.$$所以三棱锥 $E-BCD$ 的体积为\[\begin{split}V_{E-BCD}&=\dfrac 13 \cdot S_{\triangle{BCD}}\cdot DE\\&=\dfrac 13 \cdot \dfrac 12 \cdot DB\cdot DC\cdot DE\\&=\dfrac 13.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3