题目 已知椭圆 $C$ 的两个顶点分别为 $A(-2,0)$，$B(2,0)$．焦点在 $x$ 轴上，离心率为 $\dfrac{\sqrt 3}{2}$． 问题1 求椭圆 $C$ 的方程； 答案1 $\dfrac{x^2}{4}+y^2=1$ 解析1 由题知 $a=2$，$\dfrac{c}{a}=\dfrac{\sqrt 3}{2}$，所以 $c=\sqrt 3$，$b=1$，故椭圆 $C$ 的方程为 $\dfrac{x^2}{4}+y^2=1$． 备注1 问题2 点 $D$ 为 $x$ 轴上一点，过 $D$ 作 $x$ 轴的垂线交椭圆 $C$ 于不同的两点 $M,N$．过 $D$ 作 $AM$ 的垂线交 $BN$ 于点 $E$．求证：$\triangle{BDE}$ 与 $\triangle{BDN}$ 的面积之比为 $4:5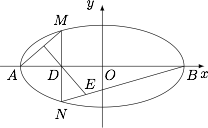$． 答案2 略 解析2 如图．<img src="/static/images/73a3a274cb2443799575e1e33cefdb22.png" class="img-responsive" /> 设 $D(2\cos\theta,0)$，$M(2\cos\theta,\sin\theta)$，$N(2\cos\theta,-\sin\theta)$．取线段 $BN$ 的一个 $5$ 等分点 $E'$（$\overrightarrow{BE}=4\overrightarrow{EN}$），则 $E'$ 的坐标为\[\left(\dfrac{2+8\cos\theta}{5},\dfrac{-4\sin\theta}{5}\right),\]进而\[\overrightarrow{E'D}\cdot \overrightarrow{AM}=\left(\dfrac{2\cos\theta-2}{5},\dfrac{4\sin\theta}{5}\right)\cdot \left(2\cos\theta+2,\sin\theta\right)=0,\]因此 $DE'\perp AM$，进而 $E'=E$，可得 $\triangle{BDE}$ 与 $\triangle{BDN}$ 的面积之比\[\dfrac{S_{\triangle BDE}}{S_{\triangle BDN}}=\dfrac{BE}{BN}=\dfrac{BE'}{BN}=\dfrac 45,\]命题得证． 备注2