如图，在四棱锥 $P-ABCD$ 中，$AB\parallel CD$，且 $\angle{BAP}=\angle{CDP}=90^{\circ}$．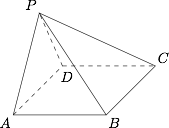
【难度】
【出处】
2017年高考全国乙卷（文）
【标注】
-
证明：$\mbox{平面}PAB\perp\mbox{平面}PAD$；标注答案略解析由已知 $\angle{BAP}=\angle{CDP}=90^{\circ}$，得 $AB\perp AP$，$CD\perp PD$．
又 $AB\parallel CD$，
所以 $AB\perp PD$，
因为 $PD\cap AP=A$，
从而 $AB\perp $ 平面 $PAD$．
又因为 $AB\subset $ 平面 $PAB$，
所以平面 $PAB\perp $ 平面 $PAD$． -
若 $PA=PD=AB=DC$，$\angle{APD}=90^{\circ}$，且四棱锥 $P-ABCD$ 的体积为 $\dfrac 83$，求该四棱锥的侧面积．标注答案$6+2\sqrt 3$解析在平面 $PAD$ 内作 $PF\perp AD$，垂足为 $F$，
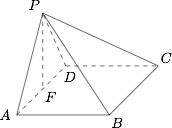由（1）可知，$AB\perp $ 平面 $PAD$，故 $AB\perp PF$，可得 $PF\perp $ 平面 $ABCD$．
设 $AB=x$，则由已知可得 $AD=\sqrt 2 x$，$PF=\dfrac{\sqrt 2}{2}x$．
故四棱锥 $P-ABCD$ 的体积$$V_{P-ABCD}=\dfrac 13 AB\cdot AD\cdot PF=\dfrac 13 x^3.$$由题设得 $\dfrac 13x^3=\dfrac 83$，故 $x=2$．
从而 $PA=PD=2$，$AD=BC=2\sqrt 2$，$PB=PC=2\sqrt 2$．
可得四棱锥 $P-ABCD$ 的侧面积为$$\dfrac 12PA\cdot PD+\dfrac 12 PA\cdot AB+\dfrac 12 PD\cdot DC+\dfrac 12 BC^2\sin{60^{\circ}}=6+2\sqrt 3.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
