由四棱柱 $ABCD-A_{1}B_{1}C_{1}D_{1}$ 截去三棱锥 $C_{1}-B_{1}CD_{1}$ 后得到的几何体如图所示．四边形 $ABCD$ 为正方形，$O$ 为 $AC$ 与 $BD$ 的交点，$E$ 为 $AD$ 的中点，$A_{1}E\perp \mbox{平面}ABCD$．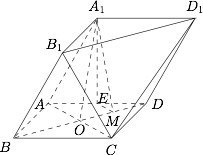
【难度】
【出处】
2017年高考山东卷（文）
【标注】
-
证明：$A_{1}O\parallel \mbox{平面}B_{1}CD$；标注答案略解析取 $B_{1}D_{1}$ 的中点 $O_{1}$，连接 $CO_{1},A_{1}O_{1}$．
由于 $ABCD-A_{1}B_{1}C_{1}D_{1}$ 是四棱柱，所以\[A_{1}O_{1}\parallel OC_{1},A_{1}O_{1}=OC,\]因此，四边形 $A_{1}OCO_{1}$ 为平行四边形，所以 $A_{1}O\parallel O_{1}C$，又 $O_{1}C\subset \text{平面}B_{1}CD_{1},A_{1}O\not \subset\text{平面}B_{1}CD_{1}$，所以 $A_{1}O\parallel \text{平面}B_{1}CD_{1}$． -
设 $M$ 是 $OD$ 的中点，证明：$\mbox{平面}A_{1}EM\perp \mbox{平面}B_{1}CD_{1}$．标注答案略解析因为 $AC\perp BD$，$E,M$ 分别为 $AD$ 和 $OD$ 的中点，所以 $EM\perp BD$，又 $A_{1}E\perp \text{平面}ABCD$，$BD\subset \text{平面}ABCD$，所以\[A_{1}E\perp BD,\]因为 $B_{1}D_{1}\parallel BD$，所以\[EM\perp B_{1}D_{1}, A_{1}E\perp B_{1}D_{1},\]又 $A_{1}E,EM\subset\text{平面}A_{1}EM$，$A_{1}E\cap EM=E$，所以 $B_{1}D_{1}\perp \text{平面}A_{1}EM$，又 $B_{1}D_{1}\perp \text{平面}B_{1}CD_{1}$，所以平面 $A_{1}EM\perp \text{平面}B_{1}CD_{1}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
