在平面直角坐标系 $xOy$ 中,已知椭圆 $C:\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0)$ 的离心率为 $\dfrac{\sqrt 2}{2}$,椭圆 $C$ 截直线 $y=1$ 所得线段的长度为 $2\sqrt 2$.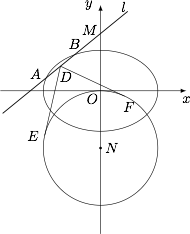

【难度】
【出处】
2017年高考山东卷(文)
【标注】
-
求椭圆 $C$ 的方程;标注答案$\dfrac{x^2}4+\dfrac{y^2}2=1$解析椭圆 $C$ 的离心率为 $\dfrac{\sqrt 2}2$,因此椭圆方程为 $\dfrac{x^2}2+y^2=b^2$,被 $y=1$ 截得的弦长\[2\sqrt{2(b^2-1)}=2\sqrt 2,\]解得 $b=\sqrt 2$,因此椭圆方程为 $\dfrac{x^2}4+\dfrac{y^2}2=1$.
-
动直线 $l:y=kx+m(m\ne 0)$ 交椭圆 $C$ 于 $A,B$ 两点,交 $y$ 轴于点 $M$.点 $N$ 是 $M$ 关于 $O$ 的对称点.$\odot N$ 的半径为 $|NO|$.设 $D$ 为 $AB$ 的中点,$DE,DF$ 与 $\odot N$ 分别相切于点 $E,F$,求 $\angle EDF$ 的最小值.标注答案$\dfrac{\pi}3$解析设 $D(x_0,y_0)$,则根据椭圆的垂径定理,可得直线 $AB$ 的斜率 $k$ 满足\[k\cdot \dfrac{y_0}{x_0}=-\dfrac 12,\]于是 $k=-\dfrac{x_0}{2y_0}$,直线 $AB$ 的方程为\[y=-\dfrac{x_0}{2y_0}\left(x-x_0\right)+y_0,\]因此 $M\left(0,\dfrac{x_0^2}{2y_0}+y_0\right)$,$N\left(0,-\dfrac{x_0^2}{2y_0}-y_0\right)$.进而\[\begin{split}\sin \angle DEN&=\dfrac{|ON|}{|DN|}\\
&=\dfrac{\dfrac{x_0^2}{2y_0}+y_0}{\sqrt{x_0^2+\left(\dfrac{x_0^2}{2y_0}+2y_0\right)^2}}\\
&=\dfrac{t+1}{\sqrt{2t+(t+2)^2}}\\
&=\sqrt{\dfrac{(t+1)^2}{(t+1)^2+4(t+1)-1}}\\
&=\sqrt{\dfrac{1}{-\left(\dfrac{1}{t+1}\right)^2+4\cdot \dfrac{1}{t+1}+1}}\\
&\overset{[a]}\geqslant \dfrac 12
,\end{split}\](推导中用到:[a])
其中 $t=\dfrac{x_0^2}{2y_0^2}$,$t\geqslant 0$.等号当且仅当 $t=0$ 时取得,因此 $\angle EDF$ 的最小值为 $\dfrac{\pi}3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2