求函数 $f(x)=\sin x\cos x+\sin x+\dfrac 25\cos x,x\in\mathbb R$ 的值域.
【难度】
【出处】
无
【标注】
【答案】
$\left[-\dfrac{76+11\sqrt{11}}{100},\dfrac{38}{25}\right]$
【解析】
考虑引入参数使用拉格朗日配方法,有\[\begin{split}f(x)&=\lambda\sin^2x+\sin x\cos x+\sin x+\lambda\cos^2x+\dfrac 25\cos x-\lambda\\&=\lambda\left(\sin x+\dfrac{\cos x+1}{2\lambda}\right)^2+\dfrac{4\lambda^2-1}{4\lambda}\left(\cos x+\dfrac{4\lambda-5}{20\lambda^2-5}\right)^2-\dfrac{100\lambda^3+4\lambda-10}{100\lambda^2-25}.\end{split}\]考虑到取等条件$$\cos x=\dfrac{5-4\lambda}{20\lambda^2-5},\quad \sin x=-\dfrac{\cos x+1}{2\lambda}=\dfrac{2-10\lambda}{20\lambda^2-5},$$有$$\left(\dfrac{5-4\lambda}{20\lambda^2-5}\right)^2+\left(\dfrac{2-10\lambda}{20\lambda^2-5}\right)^2=1,$$整理得$$100\lambda^4-79\lambda^2+20\lambda-1=0,$$解得$$\lambda=-1,\dfrac 15,\dfrac{4-\sqrt{11}}{10},\dfrac{4+\sqrt{11}}{10}.$$考虑到当两个完全平方式前的系数同号时配方才有意义,有$$\lambda\cdot\dfrac{4\lambda^2-1}{4\lambda}>0,$$即$$\lambda<-\dfrac 12$$或$$\lambda>\dfrac 12,$$因此分别取$$\lambda=-1,\lambda=\dfrac{4+\sqrt{11}}{10},$$有$$\begin{split} &\sin x\cos x+\sin x+\dfrac 25\cos x\\=&-1\left(\sin x-\dfrac 12\cos x-\dfrac 12\right)^2-\dfrac 34\left(\cos x-\dfrac 35\right)^2+\dfrac{38}{25},\end{split} $$以及\[\begin{split}&\qquad \sin x\cos x+\sin x+\dfrac 25\cos x\\&=\dfrac{4+\sqrt{11}}{10}\left(\sin x +(4-\sqrt{11})\cos x+(4-\sqrt{11})\right)^2+\dfrac{-8+3\sqrt{11}}{5}\left(\cos x+\dfrac{3-2\sqrt{11}}{10}\right)^2-\dfrac{76+11\sqrt{11}}{100},\end{split}\]于是可得 $f(x)$ 的最大值和最小值分别为 $\dfrac{38}{25}$ 以及 $-\dfrac{76+11\sqrt{11}}{100}$.
考虑到函数的连续性,可得所求函数的值域为 $\left[-\dfrac{76+11\sqrt{11}}{100},\dfrac{38}{25}\right]$,如图.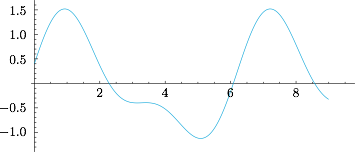
考虑到函数的连续性,可得所求函数的值域为 $\left[-\dfrac{76+11\sqrt{11}}{100},\dfrac{38}{25}\right]$,如图.

答案
解析
备注