题目 数列 $\{a_n\}$ 满足：$a_{n+1}=3a_n-3a_n^2$，$n=1,2,3,\cdots$． 问题1 若数列 $\{a_n\}$ 为常数列，求 $a_1$ 的值； 答案1 $0$ 或 $\dfrac 23$ 解析1 解不动点方程$$x=3x-3x^2,$$得$$x=0\lor x=\dfrac 23.$$于是 $a_1$ 的值为 $0$ 或 $\dfrac 23$． 备注1 问题2 若 $a_1=\dfrac 12$，求证：$\dfrac 23<a_{2n}\leqslant \dfrac 34$； 答案2 略 解析2 如图，将命题加强为$$\begin{cases}\dfrac 12\leqslant a_{2n-1} < \dfrac 23,\\\dfrac 23<a_{2n}\leqslant \dfrac 34.\end{cases}$$下面用数学归纳法证明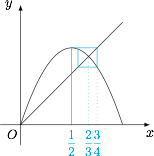．<img src="/static/images/e4267907f45f00bed9ae22adf89b91f2.png" class="img-responsive" />当 $n=1$ 时，显然有 $\dfrac 12\leqslant a_1<\dfrac 23$ 且 $\dfrac 23<a_2\leqslant \dfrac 34$；<br/>假设命题对 $n$ 成立，则由于函数 $f(x)=3x-3x^2$ 在区间 $\left[\dfrac 12,\dfrac 34\right]$ 上单调递减，于是$$f\left(\dfrac 23\right)>f\left(a_{2n}\right)\geqslant f\left(\dfrac 34\right),$$即$$\dfrac{9}{16}\leqslant a_{2n+1}<\dfrac 23,$$从而$$\dfrac 12\leqslant a_{2n+1}<\dfrac 23.$$再次利用函数 $f(x)$ 的单调性可得$$f\left(\dfrac 12\right) \geqslant f\left(a_{2n+1}\right) > f\left(\dfrac 23\right),$$即$$\dfrac 23<a_{2n+2}\leqslant \dfrac 34,$$于是命题对 $n+1$ 也成立．<br/>综上，命题得证． 备注2 问题3 在 $(2)$ 的条件下，求证：数列 $\{a_{2n}\}$ 单调递减． 答案3 略 解析3 与 $(2)$ 类似，将命题加强为数列 $\{a_{2n-1}\}$ 单调递增，且数列 $\{a_{2n}\}$ 单调递减．<br/>根据已知，$a_1=\dfrac 12$，$a_2=\dfrac 34$，$a_3=\dfrac 9{16}$，于是$$a_1<a_3\Rightarrow f(a_1)>f(a_3)\Rightarrow a_2>a_4,$$于是归纳基础得证．<br/>假设命题对 $n$ 成立，即 $a_{2n-1}<a_{2n+1}$，且 $a_{2n}>a_{2n+2}$，则有$$f\left(a_{2n}\right)<f\left(a_{2n+2}\right)\Rightarrow a_{2n+1}< a_{2n+3},$$进而$$f\left(a_{2n+1}\right)>f\left(a_{2n+3}\right) \Rightarrow a_{2n+2}>a_{2n+4},$$于是命题对 $n+1$ 也成立．<br/>综上，命题得证． 备注3 每日一题[182]迭代函数法．