题目 已知函数 $f(x)=\dfrac{1-\ln x}{x^2}$． 问题1 求函数 $f(x)$ 的零点及单调区间； 答案1 $f(x)$ 的零点为 $x={\mathrm e}$，单调递减区间为 $\left(0,{\mathrm e}^{\frac 32}\right)$，单调递增区间为 $\left({\mathrm e}^{\frac 32},+\infty\right)$ 解析1 $f(x)$ 的零点为 $x={\mathrm e}$，其导函数$$f'(x)=\dfrac{2\ln x-3}{x^3},$$于是其单调递减区间为 $\left(0,{\mathrm e}^{\frac 32}\right)$，单调递增区间为 $\left({\mathrm e}^{\frac 32},+\infty\right)$． 备注1 问题2 求证：曲线 $y=\dfrac{\ln x}{x}$ 存在斜率为 $6$ 的切线，且切点的纵坐标 $y_0<-1$． 答案2 略 解析2 注意到函数 $y=\dfrac{\ln x}{x}$ 的导函数即为 $f(x)$，画出函数草图如下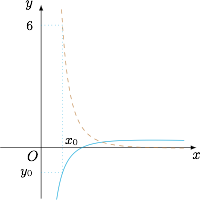．<img src="/static/images/3c3fc1780f6a3f51a0313da4f6388f77.png" class="img-responsive" />由于当 $x>\mathrm e$ 时，$f(x)<0$，且当 $x<\dfrac{1}{\mathrm e}$ 时，$f(x)>2{\mathrm e}^2$，因此在这两个区间上不存在符合题意的切线；而在区间 $\left[\dfrac{1}{\mathrm e},{\mathrm e}\right]$ 上，函数 $f(x)$ 从 $2{\mathrm e}^2$ 单调递减到 $0$，因此在该区间上存在符合题意的切线．<br/>如图，设切点的横坐标为 $x_0$，则$$\dfrac{1-\ln{x_0}}{x_0^2}=6,y_0=\dfrac{\ln x_0}{x_0},$$从第一个式子中得$$\ln x_0=1-6x_0^2,$$代入第二个式子，有$$y_0=\dfrac{1-6x_0^2}{x_0},$$用分析法不难得知欲证 $y_0<-1$，只需要证明 $x_0>\dfrac 12$．考虑到函数 $f(x)$ 在区间 $\left[\dfrac{1}{\mathrm e},{\mathrm e}\right]$ 上单调递减，因此只需要证明$$f\left(x_0\right)<f\left(\dfrac 12\right),$$即 $6<4\left(1+\ln 2\right)$，这显然成立，因此原命题得证． 备注2 每日一题[122]逐层简化．