已知椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的一个焦点为 $F(2,0)$，离心率为 $\dfrac{\sqrt 6}{3}$．过焦点 $F$ 的直线 $l$ 与椭圆 $C$ 交于 $A$、$B$ 两点，线段 $AB$ 的中点为 $D$，$O$ 为坐标原点，过 $O$、$D$ 的直线交椭圆于 $M$、$N$ 两点．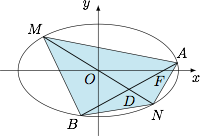
【难度】
【出处】
无
【标注】
-
求椭圆 $C$ 的方程；标注答案$C:\dfrac{x^2}{6}+\dfrac{y^2}{2}=1$解析容易求得椭圆 $C:\dfrac{x^2}{6}+\dfrac{y^2}{2}=1$；
-
求四边形 $AMBN$ 面积的最大值．标注答案$ 4\sqrt 3 $解析根据题意可得四边形 $AMBN$ 的面积$$S_{AMBN}=\dfrac 12\cdot AB\cdot MN \cdot \sin\langle AB,MN\rangle,$$其中 $AB$、$MN$ 及 $\langle AB,MN\rangle$ 均随着直线 $l$ 的运动而改变．
考虑用伸缩变换将其拉成圆，只需要将每个点的纵坐标变成原来的 $\sqrt 3$ 倍，横坐标不变即可，如图．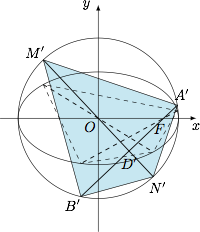
此时 $M'N'$ 为圆 $x'^2+y'^2=6$ 的直径为定值 $2\sqrt 6$，而由垂径定理 $\langle A'B',M'N'\rangle=\dfrac{\pi}{2}$ 亦为定值，此时可得$$S_{A'M'B'N'}=\sqrt 6A'B'\leqslant \sqrt 6\cdot 2\sqrt 6=12,$$等号当且仅当 $A'B'$ 为直径，也即直线 $l:y=0$ 时取得，此时四边形 $AMBN$ 的面积取得最大值$$\dfrac{S_{A'M'B'N'}}{\sqrt 3}=4\sqrt 3.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
