查看数据源：590bda1b6cddca0008611000
设已知函数 $f(x)=\left|x-a\right|-\dfrac 4x+a,a\in\mathbb{R}$．是否存在实数 $a$，使得 $f(x)=3$ 有且仅有 $3$ 个不等实根，且它们成等差数列．若存在，求出所有 $a$ 的值，若不存在，说明理由．
【难度】
【出处】
无
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    绝对值函数
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的零点
【答案】
$-\dfrac{11}{6}$ 或 $\dfrac{3}{2}\sqrt{3}+1$
【解析】
因为 $f(x)$ 的解析式含有绝对值，首先根据 $x$ 的范围去绝对值得到 $f(x)$ 的分段形式的表达式$$f(x)=\begin{cases}2a-\left(x+\dfrac 4x\right),x<a;\\x-\dfrac 4x,x\geqslant a.\end{cases}$$要研究 $f(x)=3$ 的根的情况，就需要知道函数 $y=f(x)$ 的图象与 $y=3$ 的图象的交点情况．
我们先不考虑定义域的分段点，分别研究两段对应的函数在整个定义域上的情况：
先研究不含参的函数，令$$h(x)=x-\dfrac 4x,$$则 $h(x)$ 在 $(-\infty,0)$ 与 $(0,+\infty)$ 上分别单调递增，如图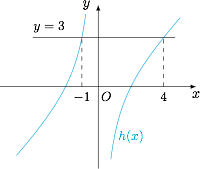：容易知道 $h(x)=3$ 有两个根 $-1$ 和 $4$；再研究另一个含参的函数，令$$g(x)=2a-\left(x+\dfrac 4x\right),$$由对勾函数的性质知 $g(x)$ 有四个单调区间，分别为 $(-\infty,-2),(-2,0),(0,2),(2,+\infty)$，草图如下：其中 $x$ 轴的位置由 $a$ 的大小决定，结合图象知 $g(x)=3$ 的根的个数可能为 $0,1,2$．
由题意知，$y=f(x)$ 的图象的“左半部分”（$(-\infty,a)$ 的部分）由 $y=g(x)$ 决定，“右半部分”（$[a,+\infty)$ 的部分）由 $y=h(x)$ 决定．$f(x)=3$ 有 $3$ 个不相等的实数根，由前面对 $h(x)$ 与 $g(x)$ 的图象的分析知，左半部分与右半部分贡献的根的个数只可能有 $1,2$ 和 $2,1$ 两种情况．
情形一若左半部分贡献 $1$ 个根，则右半部分贡献两个根 $-1,4$，由三个根呈等差数列的条件知左半部分贡献的根为 $-6$，且有 $-6<a\leqslant -1$．于是有$$g(-6)=3,$$解得$$a=-\dfrac{11}{6}.$$此时 $f(x)$ 的图象如下，容易验证此时满足题意：情形二若左半部分贡献 $2$ 个根，则右半部分只贡献一个根 $4$，从而有$$-1\leqslant a<4.$$记左半部分贡献的根为 $x_1,x_2$，且 $x_1<x_2$，则有$$x_1+4=2x_2.$$且 $x_1,x_2$ 是 $g(x)=3$ 的两个根，化简得 $x_1,x_2$ 为$$x^2+(3-2a)x+4=0$$的两根，于是有$$\begin{cases}x_1+x_2=2a-3,\\x_1x_2=4.\end{cases}$$与 $x_1+4=2x_2$ 联立解得$$\begin{cases}x_1=2(\sqrt 3-1),\\x_2=\sqrt 3+1,\\a=\dfrac 32\sqrt 3+1.\end{cases}$$或$$\begin{cases}x_1=-2(\sqrt 3+1),\\x_2=1-\sqrt 3,\\a=-\dfrac 32\sqrt 3+1.\end{cases}$$因为 $1-\sqrt 3>-\dfrac 32\sqrt 3+1(x_{2}>a)$，所以第二组数不满足要求，舍去．
综上知，$a=-\dfrac{11}{6}$ 或 $a=\dfrac{3}{2}\sqrt{3}+1$．
答案 解析 备注
0.124054s