若对任何满足 $-1\leqslant x\leqslant 1$ 的实数 $x$，都有 $\left|ax^2+bx+c\right|\leqslant 1$ 成立，求 $a$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$[-2,2]$
【解析】
分别令 $x=-1,0,1$ 得到$$\begin{cases} |a+b+c|\leqslant 1,\\|a-b+c|\leqslant 1,\\|c|\leqslant 1,\end{cases} $$于是$$|a|=\dfrac 12|(a+b+c)+(a-b+c)-2c|\leqslant 2.$$另一方面 $|2x^2-1|\leqslant 1$ 对 $x\in[-1,1]$ 恒成立，如图．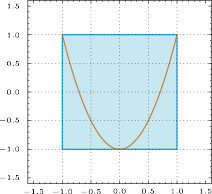
所以 $a\in[-2,2]$．
所以 $a\in[-2,2]$．
答案
解析
备注
