函数 $y=x^2+ax+b$ 的图象与坐标轴交于三个不同的点 $A$、$B$、$C$，已知 $\triangle ABC$ 的外心在直线 $y=x$ 上，求 $a+b$ 的值．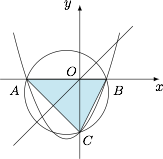
【难度】
【出处】
无
【标注】
【答案】
$ -1 $
【解析】
作出三角形 $ABC$ 的外接圆 $M$，我们发现 $M$ 实际上是过抛物线与 $x$、$y$ 轴交点的曲线，因此可以尝试用交点曲线系解决问题．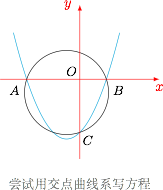
事实上，抛物线方程为$$F:x^2+ax+b-y=0,$$而 $x$、$y$ 轴的方程为$$G:xy=0,$$此时我们发现利用常规的交点曲线系 $f(x,y)+\lambda g(x,y)=0$ 得到的方程$$(x^2+ax+b-y)+\lambda\cdot xy=0$$不可能形成圆．
那么问题出在哪里？又该怎样解决呢？
由于圆的方程的特点，我们知道问题出在交叉项 $xy$ 上．因此需要仔细思考交点 $C(0,b)$ 除了用 $x=0$ 描述，是否还有其他方法？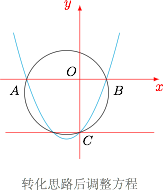
到这里，答案几乎是显然的，应该采用 $y=b$ 描述，此时可以将交点曲线系写为$$(x^2+ax+b-y)+\lambda \cdot y(y-b)=0,$$当方程表示圆时，$\lambda=1$，于是再由圆心在直线 $y=x$ 上，可得关于 $x$、$y$ 的一次项的系数相同，即$$a=-1-b,$$从而 $a+b$ 的值为 $-1$．
事实上，抛物线方程为$$F:x^2+ax+b-y=0,$$而 $x$、$y$ 轴的方程为$$G:xy=0,$$此时我们发现利用常规的交点曲线系 $f(x,y)+\lambda g(x,y)=0$ 得到的方程$$(x^2+ax+b-y)+\lambda\cdot xy=0$$不可能形成圆．那么问题出在哪里？又该怎样解决呢？
由于圆的方程的特点，我们知道问题出在交叉项 $xy$ 上．因此需要仔细思考交点 $C(0,b)$ 除了用 $x=0$ 描述，是否还有其他方法？
到这里，答案几乎是显然的，应该采用 $y=b$ 描述，此时可以将交点曲线系写为$$(x^2+ax+b-y)+\lambda \cdot y(y-b)=0,$$当方程表示圆时，$\lambda=1$，于是再由圆心在直线 $y=x$ 上，可得关于 $x$、$y$ 的一次项的系数相同，即$$a=-1-b,$$从而 $a+b$ 的值为 $-1$．
答案
解析
备注
