如图，已知平行六面体 $ABCD-A_1B_1C_1D_1$ 的底面是菱形且从顶点 $C$ 出发的三条棱两两形成的角 $\angle C_1CB=\angle C_1CD=\angle BCD=60^\circ$，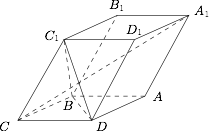
【难度】
【出处】
无
【标注】
-
证明：$C_1C\perp BD$；标注答案略解析连接 $AC$ 交 $BD$ 于 $O$，则由底面 $ABCD$ 为菱形可得对角线 $AC$ 与 $BD$ 互相垂直平分．
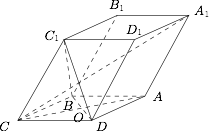由 $\triangle C_1CD$ 与 $\triangle C_1CB$ 全等，可得 $C_1D=C_1B$，进而 $\triangle C_1BD$ 为等腰三角形，于是 $C_1O\perp BD$（三线合一）．
综上，$BD\perp C_1CAA_1$，因此 $BD\perp C_1C$． -
当 $\dfrac{CD}{CC_1}$ 的值为多少时，可使 $A_1C\perp C_1BD$？标注答案$ 1 $解析由于无论 $\dfrac{CD}{CC_1}$ 的值如何变化，$A_1C$ 始终与 $BD$ 保持垂直，于是只需要使得 $A_1C$ 与平面 $C_1BD$ 内的其他与 $BD$ 不平行的直线（如 $C_1O$）垂直即可．但接下来无论是对截面 $AA_1C_1C$ 进行分析（几何）还是建立空间直角坐标系进行研究（代数）运算量都较大，我们可以采用同时融合几何与代数特性于一身的空间向量解决问题．
记 $\overrightarrow{CB}={\overrightarrow a}$，$\overrightarrow{CD}={\overrightarrow b}$，$\overrightarrow{CC_1}={\overrightarrow c}$，且它们的模分别为 $1$、$1$、$x$．令 $\overrightarrow{CA_1}\cdot \overrightarrow {C_1D}=0$ 得$$\left({\overrightarrow a}+{\overrightarrow b}+{\overrightarrow c}\right)\cdot\left({\overrightarrow b}-{\overrightarrow c}\right)=0,$$即$${\overrightarrow a}\cdot{\overrightarrow b}-{\overrightarrow a}\cdot{\overrightarrow c}+{\overrightarrow b}\cdot{\overrightarrow b}-{\overrightarrow c}\cdot{\overrightarrow c}=0,$$由已知，不难得到$$\dfrac 12-\dfrac 12x+1-x^2=0,$$解得$$x=1.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
