已知函数 $f(x)=x-{\rm e}^{\frac xa}$（$a>0$）有两个相异零点 $x_1$、$x_2$ 且 $x_1<x_2$，求证：$\dfrac{x_1}{x_2}<\dfrac{\rm e}a$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
根据已知，函数 $f(x)$ 的导函数$$f'(x)=1-\dfrac 1a{\rm e}^{\frac xa},$$于是函数 $f(x)$ 在 $\left(-\infty,a\ln a\right)$ 上单调递增，在 $\left(a\ln a,+\infty\right)$ 上单调递减，$x=a\ln a$ 是其极大值点，同时也是最大值点，而最大值为 $a\left(\ln a-1\right)$．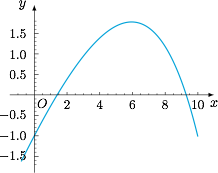
根据题意，$f(x)$ 有两个相异零点，于是有$$a\left(\ln a-1\right)>0,$$即 $a>{\rm e}$．再由 $f(0)=-1$ 可得$$0<x_1<a\ln a<x_2.\cdots (1)$$对于欲证明不等式，无法直接利用 $(1)$ 估计左边，因此利用函数 $f(x)$ 的解析式进行代换：$$\dfrac{x_1}{x_2}={\rm e}^{\frac 1a\left(x_1-x_2\right)},$$于是只需要证明$$x_2-x_1>a\ln a -a.\cdots (2)$$分析 $(2)$，在 $(1)$ 中，我们已经有了 $x_2>a\ln a$，于是一个自然的推测是尝试证明 $x_1<a$，这只需要$$f(a)=a-{\rm e}>0,$$成立即可．
综上，命题得证．
根据题意，$f(x)$ 有两个相异零点，于是有$$a\left(\ln a-1\right)>0,$$即 $a>{\rm e}$．再由 $f(0)=-1$ 可得$$0<x_1<a\ln a<x_2.\cdots (1)$$对于欲证明不等式，无法直接利用 $(1)$ 估计左边，因此利用函数 $f(x)$ 的解析式进行代换：$$\dfrac{x_1}{x_2}={\rm e}^{\frac 1a\left(x_1-x_2\right)},$$于是只需要证明$$x_2-x_1>a\ln a -a.\cdots (2)$$分析 $(2)$，在 $(1)$ 中，我们已经有了 $x_2>a\ln a$，于是一个自然的推测是尝试证明 $x_1<a$，这只需要$$f(a)=a-{\rm e}>0,$$成立即可．综上，命题得证．
答案
解析
备注
