已知函数 $f(x)=x^2+a\ln (x+1)$ 有两个相异极值点 $x_1$、$x_2$，且 $x_1<x_2$，求证：$0<\dfrac{f\left(x_2\right)}{x_1}<-\dfrac 12+\ln 2$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
根据已知，函数 $f(x)$ 的导函数$$f'(x)=2x+\dfrac{a}{x+1}=\dfrac{1}{x+1}\cdot\left(2x^2+2x+a\right),$$由题意 $f(x)$ 有两个极值点，于是$$\begin{cases}\left(2x^2+2x+a\right)_{x=-1}>0,\\\Delta=4-8a>0,\end{cases}$$解得$$0<a<\dfrac 12.$$由韦达定理，得$$x_1+x_2=-1,x_1x_2=\dfrac a2,$$于是可以将 $\dfrac{f\left(x_2\right)}{x_1}$ 化为单一变量的函数．为了避免出现根号，可以选 $x_2$ 为变量，即利用代换$$x_1=-1-x_2,a=2\left(-1-x_2\right)x_2,$$得$$\dfrac{f\left(x_2\right)}{x_1}=-\dfrac{x_2^2}{1+x_2}+2x_2\ln\left(x_2+1\right),$$并记右边关于 $x_2$ 的函数为 $g\left(x_2\right)$，其中 $x_2=\dfrac{-1+\sqrt{1-2a}}2$，取值范围是 $\left(-\dfrac 12,0\right)$．不难注意到欲证明不等式即$$g(0)<g\left(x_2\right)<g\left(-\dfrac 12\right),$$因此我们只需要证明 $g\left(x_2\right)$ 在 $\left[-\dfrac 12,0\right]$ 上单调递减．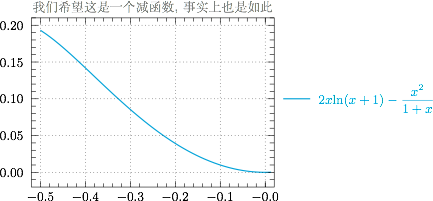
事实上，函数 $g\left(x_2\right)$ 的导函数\[\begin{split}g'_{x_2}&=2\ln \left(1+x_2\right)+\dfrac{x_2^2}{\left(1+x_2\right)^2}\\&<2x_2+\dfrac{x_2^2}{\left(1+x_2\right)^2}\\&=\dfrac{x_2\left(2x_2+1\right)\left(x_2+2\right)}{\left(1+x_2\right)^2}\\&<0,\end{split}\]于是命题得证．
事实上，函数 $g\left(x_2\right)$ 的导函数\[\begin{split}g'_{x_2}&=2\ln \left(1+x_2\right)+\dfrac{x_2^2}{\left(1+x_2\right)^2}\\&<2x_2+\dfrac{x_2^2}{\left(1+x_2\right)^2}\\&=\dfrac{x_2\left(2x_2+1\right)\left(x_2+2\right)}{\left(1+x_2\right)^2}\\&<0,\end{split}\]于是命题得证．
答案
解析
备注
