题目 设函数 $f\left(x\right)=\ln \left(x+1\right)+a\left(x^2-x\right)$，其中 $a\in\mathbb R$． 问题1 讨论函数 $f\left(x\right)$ 极值点的个数，并说明理由； 答案1 当 $a<0$ 时，函数 $f(x)$ 极值点个数为 $1$，为极大值点；<br/>当 $0\leqslant a \leqslant \dfrac 89$ 时，函数 $f(x)$ 极值点个数为 $0$；<br/>当 $a>\dfrac 89$ 时，函数的极值点个数为 $2$，其中有一个极大值点和一个极小值点 解析1 根据题意，$f(x)$ 的导函数$$f'(x)=\dfrac 1{x+1}\cdot\left( 2ax^2+ax-a+1\right) ,$$记其中决定 $f'(x)$ 符号的部分为$$h(x)=2ax^2+ax-a+1.$$考虑到二次项系数为 $2a$，于是 $a=0$ 是一个讨论点；而对称轴为 $x=-\dfrac 14$，因此需要考虑判别式$$\Delta=a^2-4\cdot 2a\cdot (-a+1)=a(9a-8),$$因此 $a=\dfrac 89$ 也是一个讨论点．于是可以根据这些讨论点进行讨论，$h(x)$ 在每个讨论区间上的图象如图所示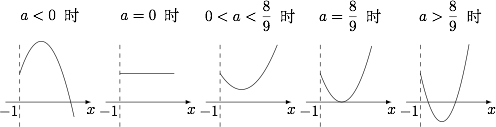．<img src="/static/images/3cb785e6b3c9d4910bd0a3c799177d0d.png" class="img-responsive" />于是不难得到：<br/>当 $a<0$ 时，函数 $f(x)$ 极值点个数为 $1$，为极大值点；<br/>当 $0\leqslant a \leqslant \dfrac 89$ 时，函数 $f(x)$ 极值点个数为 $0$；<br/>当 $a>\dfrac 89$ 时，函数的极值点个数为 $2$，其中有一个极大值点和一个极小值点． 备注1 问题2 若 $\forall x>0$，$f\left(x\right)\geqslant 0$ 成立，求 $a$ 的取值范围． 答案2 $[0,1]$ 解析2 按 $a$ 和 $0,1$ 的大小关系展开讨论，讨论中默认 $x>0$．<br/><case>情形一</case> $a<0$．<br/>令 $g(x)=\ln (x+1)-x$，则 $g(x)$ 的导函数 $g'(x)=\dfrac{1}{x+1}-1<0$，因此 $g(x)$ 单调递减，于是 $g(x)<g(0)=0$．<br/>因此 $f(x)<x+a(x^2-x)=x(ax+1-a)$，取 $x=\dfrac {1-a}{-a}$，则 $f(x)<0$，不符合题意．<br/><case>情形二</case> $0\leqslant a\leqslant 1$．<br/>此时 $f'(x)>0$，因此 $f(x)$ 单调递增，于是 $f(x)>f(0)=0$，符合题意．<br/><case>情形三</case> $a>1$．<br/>此时在区间 $\left(0,\dfrac{-a+\sqrt{a^2+8a(a-1)}}{4a}\right)$ 上有 $f'(x)<0$，因此在该区间内 $f(x)$ 单调递减，此时 $f(x)<f(0)=0$，不符合题意．<br/>综上，$a$ 的取值范围是 $[0,1]$． 备注2 每日一题[150]分析端点．<br/>每日一题[281]零点分段讨论与分析端点．