题目 设函数 $f(x)=\ln x+\dfrac{a}{{\rm e}x}$． 问题1 讨论函数 $f(x)$ 的单调性； 答案1 当 $a \leqslant 0$ 时，函数 $f(x)$ 在 $(0,+\infty )$ 上单调递增；当 $a>0$ 时，函数 $f(x)$ 在 $\left( 0,\dfrac {a}{\rm e} \right) $ 上单调递减，在 $\left( \dfrac{a}{\rm e} ,+\infty\right) $ 上单调递增 解析1 $f(x)$ 的导函数$$f'(x)=\dfrac{1}{{\rm e} x^2}\cdot ({\rm e} x-a),$$于是<br/><case>情形一</case>当 $a \leqslant 0$ 时，函数 $f(x)$ 在 $(0,+\infty )$ 上单调递增；<br/><case>情形二</case>当 $a>0$ 时，函数 $f(x)$ 在 $\left( 0,\dfrac {a}{\rm e} \right) $ 上单调递减，在 $\left( \dfrac{a}{\rm e} ,+\infty\right) $ 上单调递增． 备注1 问题2 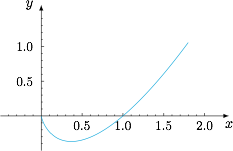若 $a=2$，证明：对任意的 $x>0$，都有 $f(x)>{\rm e} ^{-x}$． 答案2 略 解析2 题中的不等式即$$\ln x+\dfrac{2}{{\rm e}x}>{\rm e}^{-x},$$也即$$x\ln x+\dfrac 2{\rm e}>{\rm e}^{-x}\cdot x,$$设函数 $h(x)=x\ln x$，那么我们有$$h\left( {\rm e}^{-x}\right) =-{\rm e}^{-x}\cdot x,$$于是该不等式即$$h(x)+h \left( {\rm e} ^{-x}\right) \geqslant -\dfrac 2{\rm e}.$$发现题中指数部分和对数部分之间的关联后，研究其中的桥梁- $h(x)$ 就是势在必行的了．事实上，$h(x)$ 的导函数$$h'(x)=1+\ln x,$$于是函数 $h(x)$ 的草图如图，在 $(0,+\infty )$ 上最小值为$$h\left( \dfrac 1{\rm e} \right) =-\dfrac 1{\rm e}.$$<img src="/static/images/f788d298e5fd5cc48dca5c09023d2521.png" class="img-responsive" />由于当 $x>0$ 时，${\rm e} ^{-x}$ 取遍所有 $(0,1)$ 上的实数，于是 $h \left( {\rm e} ^{-x}\right) $ 的取值范围是 $\left[-\dfrac 1{\rm e} ,0\right) $．这样我们就得到了$$h(x)\geqslant -\dfrac 1{\rm e} \land h\left( {\rm e} ^{-x}\right) \geqslant -\dfrac 1{\rm e} ,$$但两个式子中的等号分别当且仅当 $x=\dfrac 1{\rm e} $ 和 $x=1$ 时取得，无法同时取得，因此我们就得到了题中的不等式． 备注2 解题中用到了这个简单事实：<br/><sol>引理</sol>一个复合函数 $f \left( g(x)\right) $ 的取值范围是函数 $f(x)$ 的值域的子集，特别的，如果函数 $g(x)$ 的取值范围恰好与 $f(x)$ 的定义域相同，那么复合函数 $f \left( g(x)\right) $ 的取值范围就是函数 $f(x)$ 的值域．<br/>利用引理，我们可以通过一种新颖的方式证明：<br/>如果函数 $f(x)=x+\dfrac 1x$，其中 $x>0$ 有最小值 $m$，那么 $m=2$．<br/><sol>证明</sol>考虑函数 $\left[f(x)\right]^2$．<br/>一方面，其最小值为 $m^2$；另一方面，有$$\left[f(x)\right]^2=x^2+\dfrac{1}{x^2}+2=f \left( x^2\right) +2,$$而当 $x$ 取遍所有正实数时，$x^2$ 也取遍所有正实数，因此其最小值为 $m+2$；综上，可以得到$$m^2=m+2,$$解得 $m=2,$ 其中 $m=-1$ 舍去．<br/>每日一题[282]天堑变通途．