设点 $O$ 为椭圆的中心,点 $A$ 为椭圆上异于顶点的任意一点,过点 $A$ 作长轴的垂线,垂足为 $M$,连接 $AO$ 并延长交椭圆于另一点 $B$,连接 $BM$ 并延长交椭圆于点 $C$,问是否存在椭圆,使得 $BA\perp CA$?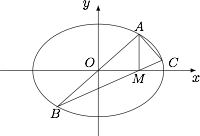

【难度】
【出处】
2014年全国高中数学联赛山东省预赛
【标注】
【答案】
存在
【解析】
假设存在满足条件的椭圆,设椭圆方程为 $\dfrac {x^2}{a^2}+\dfrac{y^2}{b^2}=1$.记 $A(m,n)$,$B(-m,-n)$,$M(m,0)$,则根据椭圆的"垂径定理",有$$k_{CA}\cdot k_{CB}=-\dfrac{b^2}{a^2},$$而$$k_{CA}=-\dfrac{1}{k_{AB}}=-\dfrac mn,$$且$$k_{CB}=k_{BM}=\dfrac{n}{2m},$$于是可得$$\left(-\dfrac mn\right)\cdot\dfrac{n}{2m}=-\dfrac{b^2}{a^2},$$化简得$$a^2=2b^2.$$因此存在符合题意的椭圆使得 $BA\perp CA$,只需椭圆的离心率为 $\dfrac{\sqrt 2}2$ 即可.
答案
解析
备注