如图，动点 $M$ 与两定点 $A(-1,0)$、$B(2,0)$ 构成三角形 $MAB$，且 $\angle MBA=2\angle MAB$，设动点 $M$ 的轨迹为 $C$．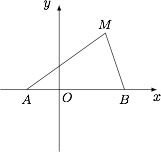
【难度】
【出处】
2012年高考四川卷（理）
【标注】
-
求轨迹 $C$ 的方程；标注答案$x^2-\dfrac{y^2}{3}=1,x>1$解析注意到倍角条件，可以作角平分线构造等腰三角形转化条件．
作 $\angle MBA$ 的角平分线交 $MA$ 于 $D$，过 $D$ 作 $x$ 轴的垂线，垂足为 $E$，过 $M$ 作 $DE$ 的垂线，垂足为 $H$，如图．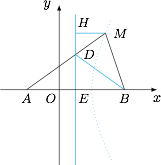
根据已知条件可得 $\angle DAB=\angle DBA$，于是 $DE$ 为线段 $AB$ 的垂直平分线，为定直线 $x=\dfrac 12$．由角平分线定理，可得$$\dfrac{BM}{BA}=\dfrac{DM}{DA},$$再由三角形 $DMH$ 与三角形 $DAE$ 相似可得$$\dfrac{DM}{DA}=\dfrac{MH}{AE},$$于是$$\dfrac{BM}{BA}=\dfrac{MH}{AE},$$从而$$\dfrac{MB}{MH}=\dfrac{BA}{AE}=2$$为定值．
进而由双曲线的第二定义不难得到所求的轨迹方程为$$x^2-\dfrac{y^2}{3}=1,x>1.$$ -
设直线 $y=-2x+m$ 与 $y$ 轴相交于点 $P$，与轨迹 $C$ 相交于点 $Q$、$R$，且 $|PQ|<|PR|$，求 $\dfrac{|PR|}{|PQ|}$ 的取值范围．标注答案$\left(1,7\right)\cup\left(7,7+4\sqrt 3\right)$解析设 $Q\left(x_1,y_1\right)$，$R\left(x_2,y_2\right)$，$\dfrac{x_2}{x_1}=\lambda$，$\lambda>1$．联立直线与双曲线方程，可得$$x^2-4mx+m^2+3=0,$$该方程在 $(1,+\infty)$ 内有两个相异实根，于是可得 $m>1\land m\neq 2$．根据韦达定理，有$$\left(4m\right)^2=\left(2+\lambda+\dfrac{1}{\lambda}\right)\cdot\left(m^2+3\right),$$化简得$$\lambda+\dfrac{1}{\lambda}=\dfrac{16m^2}{m^2+3}-2,$$于是 $\lambda+\dfrac{1}{\lambda}$ 的取值范围是 $\left(2,\dfrac{50}{7}\right)\cup\left(\dfrac{50}{7},14\right)$，进而不难得到 $\lambda$ 的取值范围是 $\left(1,7\right)\cup\left(7,7+4\sqrt 3\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
