若存在集合 $A,B$ 满足：$A\cap B=\varnothing$，且 $A\cup B=\mathbb N^*$，则称 $(A,B)$ 为 $\mathbb N^*$ 的一个二分划．
【难度】
【出处】
2014年全国高中数学联赛吉林省预赛
【标注】
-
设 $A=\left\{x\left| \right.x=3k,k\in \mathbb N^*\right\}$，$B=\left\{x\left|\right.x=3k\pm 1,k\in \mathbb N^*\right\}$，判断 $(A,B)$ 是否为 $\mathbb N^*$ 的一个二分划；标注答案不是解析不是．
-
是否能找到 $\mathbb N^*$ 的一个二分划 $(A,B)$ 满足：
① $A$ 中不存在三个成等比数列的数；
② $B$ 中不存在无穷的等比数列．说明理由．标注答案能解析一个使得其中不存在三个成等比数列的数的取法为递增序列：$$a_1,a_2,a_3,\cdots,a_n,\cdots,$$满足$$\forall n\in\mathbb N^*,a_{n+2}>\dfrac{a_{n+1}^2}{a_n},$$此时$$\forall n\in\mathbb N^*,a_{n+1}<\dfrac{a_n+a_{n+2}}2,$$于是 $n-a_n$ 的散点图下凸，此时不存在任何共线的三个点，当然也不存在任何三项成等差数列．
接下来我们将正整数集中的无穷等比数列按首项 $a$ 和公比 $q$ 简记为 $(a,q)$，将所有无穷等比数列排成\[\begin{matrix}&(1,2)\quad &(1,3) \quad &(1,4)\quad &\cdots \\&(2,2)\quad &(2,3) \quad &(2,4)\quad &\cdots \\&(3,2)\quad &(3,3) \quad &(3,4)\quad &\cdots\\&\cdots \quad &\cdots\quad &\cdots \quad &\cdots \end{matrix}\]继而遍历所有的无穷等比数列，并分别从每个无穷等比数列中抽一个满足之前所述性质的数构成序列 $a_1,a_2,a_3,\cdots$，如图．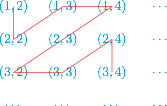
比如，可以取 $A=\left\{1,2,9,64,1458,\cdots\right\}$．这样就完成了分划 $(A,B)$ 的构造．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
