在平面直角坐标系中,两点 $P_1(x_1,y_1)$,$P_2(x_2,y_2)$ 间的"L-距离"定义为 $||P_1P_2||=\left|x_1-x_2\right|+\left|y_1-y_2\right|$,求平面内与 $x$ 轴上两个不同的定点 $F_1(-1,0)$,$F_2(1,0)$ 的"L-距离"之和等于 $5$ 的点的轨迹所围成的面积.
【难度】
【出处】
无
【标注】
【答案】
$10$
【解析】
如图.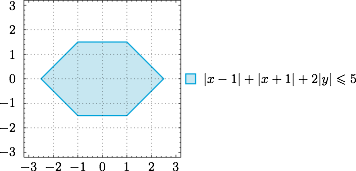

答案
解析
备注