已知 $a,b$ 均为正实数，且 $a^4+b^2=5$，求 $a+b$ 的最大值．
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
先利用导数处理函数 $f(x)=x+\sqrt{5-x^4}$．$f(x)$ 的定义域为 $\left[-5^{\frac 14},5^{\frac 14}\right]$．
当 $x<0$ 时，$f(x)$ 单调递增；
当 $x\geqslant 0$ 时，导函数$$ f'(x)=1+\dfrac 12\left(5-x^4\right)^{-\frac 12}\cdot (-4x^3)=\dfrac{1}{\sqrt{5-x^4}}\cdot \left(\sqrt{5-x^4}-2x^3\right),$$令$$g(x)=\sqrt{5-x^4}-2x^3,x\geqslant 0$$则 $g(x)$ 单调递减，且有唯一零点为 $x=1$．
于是函数 $f(x)$ 在 $x=1$ 处取得极大值，亦为最大值 $3$．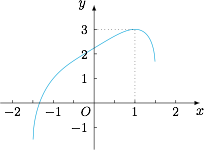
当然，我们也可以求出 $f(x)$ 的最小值，函数在定义域区间端点处取得最小值，经比较可得最小值为$$\left.y\right|_{x=-5^{\frac 14}}=-5^{\frac 14}.$$从而我们得到函数的值域为 $\left[-5^{\frac 14},3\right]$．
当 $x<0$ 时，$f(x)$ 单调递增；
当 $x\geqslant 0$ 时，导函数$$ f'(x)=1+\dfrac 12\left(5-x^4\right)^{-\frac 12}\cdot (-4x^3)=\dfrac{1}{\sqrt{5-x^4}}\cdot \left(\sqrt{5-x^4}-2x^3\right),$$令$$g(x)=\sqrt{5-x^4}-2x^3,x\geqslant 0$$则 $g(x)$ 单调递减，且有唯一零点为 $x=1$．
于是函数 $f(x)$ 在 $x=1$ 处取得极大值，亦为最大值 $3$．
当然，我们也可以求出 $f(x)$ 的最小值，函数在定义域区间端点处取得最小值，经比较可得最小值为$$\left.y\right|_{x=-5^{\frac 14}}=-5^{\frac 14}.$$从而我们得到函数的值域为 $\left[-5^{\frac 14},3\right]$．
答案
解析
备注
