已知椭圆 $\dfrac {x^2}{4}+\dfrac {y^2}{3}=1$,点 $P(4,0)$,过点 $P$ 作椭圆的割线 $PAB$,$C$ 为 $B$ 关于 $x$ 轴的对称点.求证:直线 $AC$ 恒过定点.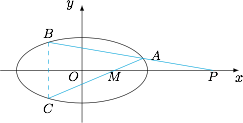

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
因为 $A,B,P$ 三点共线,$A,C,M$ 三点也共线,且 $A,B,C$ 三点都在椭圆上,我们用定比点差法去解决这个问题.
设 $A(x_1,y_1)$,$B(x_2,y_2)$,则 $C(x_2,-y_2)$,设 $AC$ 与 $x$ 轴的交点为 $M(m,0)$,$\overrightarrow{AP}=\lambda \overrightarrow{PB}$,$\overrightarrow {AM}=\mu\overrightarrow {MC}$,则$$P\left(\dfrac {x_1+\lambda x_2}{1+\lambda},\dfrac {y_1+\lambda y_2}{1+\lambda }\right ),M\left(\dfrac {x_1+\mu x_2}{1+\mu },\dfrac {y_1-\mu y_2}{1+\mu}\right ).$$于是有$$ x_1+\lambda x_2=4(1+\lambda ),y_1+\lambda y_2=0;\cdots (1)$$$$x_1+\mu x_2=m(1+\mu),y_1-\mu y_2=0.\cdots(2)$$由点 $A,B$ 在椭圆上得$$\begin{cases} \dfrac {x_1^2}{4}+\dfrac {y_1^2}{3}=1,\\\dfrac {\mu^2x_2^2}{4}+\dfrac {\mu^2y_2^2}{3}=\mu^2.\end{cases}$$两式相减得$$\dfrac {(x_1+\mu x_2)(x_1-\mu x_2)}{4}+\dfrac {(y_1+\mu y_2)(y_1-\mu y_2)}{3}=1-\mu ^2.\cdots (3)$$将 $(2)$ 代入 $(3)$ 得$$ x_1-\mu x_2=\dfrac {4(1-\mu)}{m}.\cdots(4)$$由 $(1)$ $(2)$ 得 $\mu=-\lambda $,代入 $(4)$ 得$$x_1+\lambda x_2=\dfrac {4(1+\lambda )}{m}.$$与 $(1)$ 对比得 $m=1$,即直线 $AC$ 恒过定点 $(1,0)$.
设 $A(x_1,y_1)$,$B(x_2,y_2)$,则 $C(x_2,-y_2)$,设 $AC$ 与 $x$ 轴的交点为 $M(m,0)$,$\overrightarrow{AP}=\lambda \overrightarrow{PB}$,$\overrightarrow {AM}=\mu\overrightarrow {MC}$,则$$P\left(\dfrac {x_1+\lambda x_2}{1+\lambda},\dfrac {y_1+\lambda y_2}{1+\lambda }\right ),M\left(\dfrac {x_1+\mu x_2}{1+\mu },\dfrac {y_1-\mu y_2}{1+\mu}\right ).$$于是有$$ x_1+\lambda x_2=4(1+\lambda ),y_1+\lambda y_2=0;\cdots (1)$$$$x_1+\mu x_2=m(1+\mu),y_1-\mu y_2=0.\cdots(2)$$由点 $A,B$ 在椭圆上得$$\begin{cases} \dfrac {x_1^2}{4}+\dfrac {y_1^2}{3}=1,\\\dfrac {\mu^2x_2^2}{4}+\dfrac {\mu^2y_2^2}{3}=\mu^2.\end{cases}$$两式相减得$$\dfrac {(x_1+\mu x_2)(x_1-\mu x_2)}{4}+\dfrac {(y_1+\mu y_2)(y_1-\mu y_2)}{3}=1-\mu ^2.\cdots (3)$$将 $(2)$ 代入 $(3)$ 得$$ x_1-\mu x_2=\dfrac {4(1-\mu)}{m}.\cdots(4)$$由 $(1)$ $(2)$ 得 $\mu=-\lambda $,代入 $(4)$ 得$$x_1+\lambda x_2=\dfrac {4(1+\lambda )}{m}.$$与 $(1)$ 对比得 $m=1$,即直线 $AC$ 恒过定点 $(1,0)$.
答案
解析
备注