在扇形 $AOB$ 中，$OA=OB=1$，$\angle AOB=\dfrac{\pi}3$，$C$ 为弧 $AB$（不包含端点）上的一点，且 $\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$．
【难度】
【出处】
无
【标注】
-
求 $x+y$ 的取值范围；标注答案$\left(1,\dfrac{2\sqrt 3}3\right]$解析利用等系数和线可以方便地处理很多与系数和有关的问题．
示意图如下．
如图，$C$ 所在的弧 $AB$ 在 $m=1$ 和 $m=\dfrac 2{\sqrt 3}$ 的两条等系数和线之间（包括 $MN$，不包括 $AB$），于是 $x+y$ 的取值范围是 $\left(1,\dfrac{2\sqrt 3}3\right]$． -
若 $t=x+\lambda y$ 存在最大值，求 $\lambda$ 的取值范围．标注答案$\left(\dfrac 12,2\right)$解析如图，将已知条件改写为$$\overrightarrow{OC}=x\overrightarrow{OA}+\lambda y\left(\dfrac 1{\lambda}\overrightarrow{OB}\right),$$于是 $t$ 所对应的等系数和线是一系列与直线 $AP$ 平行的直线，其中 $P$ 为向量 $\dfrac 1{\lambda}\overrightarrow{OB}$ 的终点．
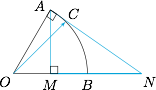由于 $t$ 有最大值，于是其对应的一系列等系数和线中必然存在与弧 $AB$ 相切的一条，因此 $P$ 位于线段 $MN$ 上（不包括端点），其中 $AM$ 与 $B$ 处的切线平行，$AN$ 为 $A$ 处的切线．从而易得 $\lambda$ 的取值范围是 $\left(\dfrac 12,2\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
