已知 $O$ 为锐角三角形 $ABC$ 的外心，$A=\dfrac{\pi}3$，且 $\overrightarrow{OA}=x\overrightarrow{OB}+y\overrightarrow{OC}$，求 $2x-y$ 的取值范围．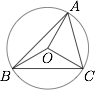
【难度】
【出处】
无
【标注】
【答案】
$(-2,1)$
【解析】
设 $BD$ 和 $CE$ 为圆 $O$ 的直径，则点 $A$ 在劣弧 $DE$ 上运动，于是$$\overrightarrow {OA}=(-x)\overrightarrow{OD}+(-y)\overrightarrow{OE}, \land x,y<0.$$
考虑到问题涉及的代数式为 $2x-y$，为了利用向量分解的系数和的几何意义（可以参考每日一题[426] 向量分解的系数和），将条件转化为$$\overrightarrow{OA}=2x\left(-\dfrac 12\overrightarrow{OD}\right)+(-y)\overrightarrow{OE},$$此时可知连接向量 $-\dfrac 12\overrightarrow{OD}$ 的终点 $F$ 与向量 $\overrightarrow{OE}$ 的终点 $E$ 的直线 $EF$ 即等系数和线$$2x-y=1,$$如图．
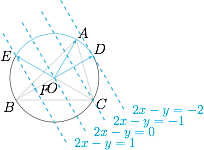依次作出其余等系数和线，可得 $2x-y$ 的取值范围是 $(-2,1)$．
考虑到问题涉及的代数式为 $2x-y$，为了利用向量分解的系数和的几何意义（可以参考每日一题[426] 向量分解的系数和），将条件转化为$$\overrightarrow{OA}=2x\left(-\dfrac 12\overrightarrow{OD}\right)+(-y)\overrightarrow{OE},$$此时可知连接向量 $-\dfrac 12\overrightarrow{OD}$ 的终点 $F$ 与向量 $\overrightarrow{OE}$ 的终点 $E$ 的直线 $EF$ 即等系数和线$$2x-y=1,$$如图．依次作出其余等系数和线，可得 $2x-y$ 的取值范围是 $(-2,1)$．
答案
解析
备注
