将边长为 $1$ 的正三角形沿经过其中心的直线对折，求对折后的纸片所能覆盖的最大面积．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{\sqrt 3}{6}$
【解析】
将对折后的纸片沿对折时使用的直线作对称可以得到所求面积的两倍为正三角形纸片的面积再加上三个小三角形的面积，如图．
可以依次证明相邻的两个小三角形全等：
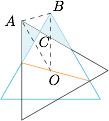连接 $AB$，因为 $\triangle OAB$ 为等腰三角形，所以底角相等，从而有$$\angle CAB=\angle CBA,$$所以 $\triangle CAB$ 为等腰三角形，$CA=CB$，从而得到相邻的这两个小三角形全等．其它全等类似可证．
设小三角形的 $60^\circ$ 角的两角邻边长分别为 $a,b$，则有$$a+b+\sqrt{a^2+b^2-2ab\cos 60^\circ}=a+b+\sqrt{a^2+b^2-ab}=1,$$小三角形的面积记为 $S$，有$$S=\dfrac 12ab\sin 60^\circ=\dfrac {\sqrt 3}4ab,$$而所求面积为$$\dfrac 12\left(\dfrac {\sqrt 3}4+3S\right),$$所以求 $S$ 的最大值即可．
由均值不等式有$$1=a+b+\sqrt{a^2+b^2-ab}\geqslant 2\sqrt{ab}+\sqrt{ab},$$所以 $ab\leqslant 1/9$，当且仅当 $a=b$ 时取到等号．于是所求最大值为$$ \dfrac 12\left(\dfrac {\sqrt 3}4+3\cdot \dfrac{\sqrt 3}4\cdot \dfrac 19\right)=\dfrac {\sqrt 3}6.$$
可以依次证明相邻的两个小三角形全等：连接 $AB$，因为 $\triangle OAB$ 为等腰三角形，所以底角相等，从而有$$\angle CAB=\angle CBA,$$所以 $\triangle CAB$ 为等腰三角形，$CA=CB$，从而得到相邻的这两个小三角形全等．其它全等类似可证．设小三角形的 $60^\circ$ 角的两角邻边长分别为 $a,b$，则有$$a+b+\sqrt{a^2+b^2-2ab\cos 60^\circ}=a+b+\sqrt{a^2+b^2-ab}=1,$$小三角形的面积记为 $S$，有$$S=\dfrac 12ab\sin 60^\circ=\dfrac {\sqrt 3}4ab,$$而所求面积为$$\dfrac 12\left(\dfrac {\sqrt 3}4+3S\right),$$所以求 $S$ 的最大值即可．
由均值不等式有$$1=a+b+\sqrt{a^2+b^2-ab}\geqslant 2\sqrt{ab}+\sqrt{ab},$$所以 $ab\leqslant 1/9$，当且仅当 $a=b$ 时取到等号．于是所求最大值为$$ \dfrac 12\left(\dfrac {\sqrt 3}4+3\cdot \dfrac{\sqrt 3}4\cdot \dfrac 19\right)=\dfrac {\sqrt 3}6.$$
答案
解析
备注
