某校 $ 100 $ 名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:$\left[ {50,60} \right)$,$\left[ {60,70} \right)$,$\left[ {70,80} \right)$,$\left[ {80,90} \right)$,$\left[ {90,100} \right]$.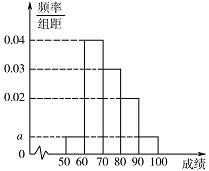

【难度】
【出处】
2012年高考广东卷(文)
【标注】
-
求图中 $a$ 的值;标注答案$ a = 0.005 $解析考查频率分布直方图.\[\left(2a + 0.02 + 0.03 + 0.04\right) \times 10 = 1 \Rightarrow a = 0.005.\]
-
根据频率分布直方图,估计这 $ 100 $ 名学生语文成绩的平均分;标注答案估计这 $ 100 $ 名学生语文成绩的平均分为 $ 73 $解析考查样本的数字特征.平均分为\[55 \times 0.05 + 65 \times 0.4 + 75 \times 0.3 + 85 \times 0.2 + 95 \times 0.05 = 73.\]
-
若这 $ 100 $ 名学生语文成绩某些分数段的人数 $\left(x\right)$ 与数学成绩相应分数段的人数 $\left(y\right)$ 之比如下表所示,求数学成绩在 $\left[ {50 , 90} \right)$ 之外的人数.\[\begin{array}{|c|c|c|c|c|}\hline
{分数段}&\left[50,60\right)&\left[60,70\right)&\left[70,80\right)&\left[80,90\right)\\ \hline
{x:y}&1:1&2:1&3:4&4:5\\ \hline
\end{array}\]标注答案数学成绩在 $\left[50,90\right)$ 外的人数为 $100 - 90 = 10$ 人解析先求成绩在 $\left[50,90\right)$ 内的人数,再用总人数减之即可.数学成绩在 $\left[50,90\right)$ 内的人数为\[\left(0.005 + \dfrac{1}{2} \times 0.04 + \dfrac{4}{3} \times 0.03 + \dfrac{5}{4} \times 0.02\right) \times 10 \times 100 = 90,\]故数学成绩在 $\left[50,90\right)$ 外的人数为 $100 - 90 = 10$ 人.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3