若函数 $f(x)=x\ln x-ax^2-x+1$ 存在最大值，求 $a$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$\left(0,\dfrac{1}{{\rm e}^2}\right]$
【解析】
考虑 $f(x)$ 的导函数$$f'(x)=\ln x-2ax=x\left(\dfrac{\ln x}{x}-2a\right),$$考虑函数 $y=\dfrac{\ln x}{x}$ 与直线 $y=2a$ 的交点情况，如图．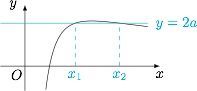
这里用到了 $\left(\dfrac{\ln x}{x}\right)'=\dfrac{1-\ln x}{x^2}$．
当 $2a\geqslant \dfrac 1{\rm e}$ 时，$f'(x)\leqslant 0$，无最大值；
当 $0<2a<\dfrac{1}{\rm e}$ 时，设两个交点满足$$0<x_1<{\rm e}<x_2,$$则函数 $f(x)$ 有最大值只需要$$f(x_2)\geqslant \lim_{x\to 0+}{f(x)}=1,$$即$$x_2\ln{x_2}-ax_2^2-x_2+1\geqslant 1,$$由 $\dfrac{\ln x_2}{x_2}=2a$，于是上述不等式即$$x_2\geqslant \dfrac 1a,$$由于函数 $y=\dfrac{\ln x}x$ 在 $x>{\rm e}$ 上是单调递减函数，因此上述不等式等价于$$2a=\dfrac{\ln x_2}{x_2}\leqslant -a\ln a,$$解得 $a\leqslant \dfrac{1}{{\rm e}^2}$．因此所求 $a$ 的取值范围是 $\left(0,\dfrac{1}{{\rm e}^2}\right]$．
这里用到了 $\left(\dfrac{\ln x}{x}\right)'=\dfrac{1-\ln x}{x^2}$．当 $2a\geqslant \dfrac 1{\rm e}$ 时，$f'(x)\leqslant 0$，无最大值；
当 $0<2a<\dfrac{1}{\rm e}$ 时，设两个交点满足$$0<x_1<{\rm e}<x_2,$$则函数 $f(x)$ 有最大值只需要$$f(x_2)\geqslant \lim_{x\to 0+}{f(x)}=1,$$即$$x_2\ln{x_2}-ax_2^2-x_2+1\geqslant 1,$$由 $\dfrac{\ln x_2}{x_2}=2a$，于是上述不等式即$$x_2\geqslant \dfrac 1a,$$由于函数 $y=\dfrac{\ln x}x$ 在 $x>{\rm e}$ 上是单调递减函数，因此上述不等式等价于$$2a=\dfrac{\ln x_2}{x_2}\leqslant -a\ln a,$$解得 $a\leqslant \dfrac{1}{{\rm e}^2}$．因此所求 $a$ 的取值范围是 $\left(0,\dfrac{1}{{\rm e}^2}\right]$．
答案
解析
备注
