设 $F_1,F_2$ 是椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的焦点，椭圆的弦 $AB$ 过焦点 $F_1$，求 $\triangle ABF_2$ 面积的最大值．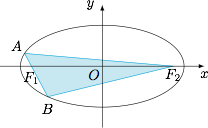
【难度】
【出处】
无
【标注】
【答案】
当 $a\geqslant \sqrt 2b$ 时，所求面积的最大值为 $ab$；当 $a<\sqrt 2b$ 时，所求面积的最大值为 $\dfrac{2b^2\sqrt{a^2-b^2}}a$
【解析】
考虑将椭圆变成圆解决问题，如图，将所有点的纵坐标变为原来的 $\dfrac ab$ 倍，则$$S_{\triangle ABF_2}=\dfrac ba\cdot S_{\triangle A'B'F_2},$$于是只需要求圆中 $\triangle A'B'F_2$ 的面积的最大值．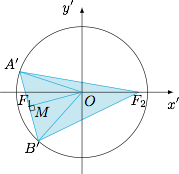
连接 $OA',OB'$，取 $A'B'$ 的中点 $M$，设 $OM=d$，则 $d\in\left(0,c\right]$，其中 $c=\sqrt{a^2-b^2}$，且$$S_{\triangle A'B'F_2}=2S_{\triangle A'B'O}=2\cdot \sqrt{d^2(a^2-d^2)},$$若 $c\geqslant \dfrac{a}{\sqrt 2}$，即 $e\geqslant \dfrac {\sqrt 2}2$，则$$S_{\triangle ABF_2}\leqslant \dfrac ba\cdot 2\cdot\dfrac{(a^2-d^2)+d^2}2 =ab;$$若 $c<\dfrac{a}{\sqrt 2}$，即 $e<\dfrac{\sqrt 2}2$，则$$S_{\triangle ABF_2}\leqslant \dfrac ba\cdot 2\cdot\sqrt{(a^2-c^2)c^2}=\dfrac{2b^2c}a=\dfrac{2b^2\sqrt{a^2-b^2}}a.$$综上所述，当 $a\geqslant \sqrt 2b$ 时，所求面积的最大值为 $ab$；当 $a<\sqrt 2b$ 时，所求面积的最大值为 $\dfrac{2b^2\sqrt{a^2-b^2}}a$．
连接 $OA',OB'$，取 $A'B'$ 的中点 $M$，设 $OM=d$，则 $d\in\left(0,c\right]$，其中 $c=\sqrt{a^2-b^2}$，且$$S_{\triangle A'B'F_2}=2S_{\triangle A'B'O}=2\cdot \sqrt{d^2(a^2-d^2)},$$若 $c\geqslant \dfrac{a}{\sqrt 2}$，即 $e\geqslant \dfrac {\sqrt 2}2$，则$$S_{\triangle ABF_2}\leqslant \dfrac ba\cdot 2\cdot\dfrac{(a^2-d^2)+d^2}2 =ab;$$若 $c<\dfrac{a}{\sqrt 2}$，即 $e<\dfrac{\sqrt 2}2$，则$$S_{\triangle ABF_2}\leqslant \dfrac ba\cdot 2\cdot\sqrt{(a^2-c^2)c^2}=\dfrac{2b^2c}a=\dfrac{2b^2\sqrt{a^2-b^2}}a.$$综上所述，当 $a\geqslant \sqrt 2b$ 时，所求面积的最大值为 $ab$；当 $a<\sqrt 2b$ 时，所求面积的最大值为 $\dfrac{2b^2\sqrt{a^2-b^2}}a$．
答案
解析
备注
