已知椭圆 $C$ 的中心在平面直角坐标系 $xOy$ 的原点，一个焦点是 $\left(0,\sqrt2\right)$，且长轴与短轴的长度比是 $\sqrt2:1$．$C$ 上在第一象限的点 $P$ 的横坐标为 $1$，过点 $P$ 作两条倾斜角互补的直线，分别交 $C$ 于另外两点 $A,B$．求：
【难度】
【出处】
2014年第二十五届“希望杯”全国数学邀请赛高二（二试）
【标注】
-
$C$ 的方程；标注答案$\dfrac{y^2}{4}+\dfrac{x^2}{2}=1$解析由题可知焦点在 $y$ 轴上，设方程为 $\dfrac{y^2}{a^2}+\dfrac{x^2}{b^2}=1(a>b>0)$，则有$$c=\sqrt2,\dfrac{a}{b}=\sqrt2,$$解得 $a=2,b=\sqrt2$，因此方程为 $\dfrac{y^2}{4}+\dfrac{x^2}{2}=1$．
-
直线 $AB$ 的斜率；标注答案$\sqrt2$解析对椭圆进行如下放射变换$$\begin{cases}x'=\sqrt2x,\\y'=y,\end{cases}$$此时椭圆方程化为$$x^2+y^2=4,$$表示以原点为圆心半径为 $2$ 的圆，如图．
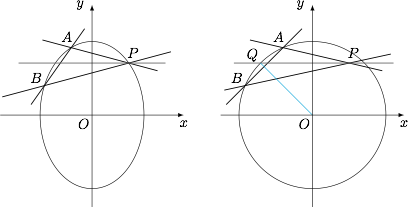设点 $A(x_1,y_1),B(x_2,y_2)$，且 $P(1,\sqrt2)$，则仿射变换后，对应的点为$$A'(\sqrt2x_1,y_1),B'(\sqrt2x_2,y_2),P'\left(\sqrt2,\sqrt2\right),$$由 $PA,PB$ 倾斜角互补，则 $PA',PB'$ 倾斜角也互补，则点 $Q\left(-\sqrt2,\sqrt2\right)$ 是 $\overparen{AB}$ 的中点，根据“垂径定理”，得$$k_{A'B'}\cdot k_{OQ}=-1,$$所以，有$$k_{AB}=\dfrac{y_2-y_1}{x_2-x_1}=\sqrt2k_{A'B'}=\sqrt2,$$因此，直线 $AB$ 的斜率为 $\sqrt2$． -
$\triangle PAB$ 面积的最大值．标注答案$\sqrt2$解析设直线 $AB$ 方程为 $y=\sqrt2x+m$，联立椭圆，消去 $y$，得$$4x^2+2\sqrt2mx+m^2-4=0,$$由题可知$$\Delta=8(-m^2+8)>0,$$因此，$m^2<8$，此时有韦达定理$$\begin{cases}x_1+x_2=\dfrac{-\sqrt2m}{2},\\x_1x_2=\dfrac{m^2-4}{4},\end{cases}$$因此，$\triangle PAB$ 的面积为\[\begin{split}S_{\triangle PAB}&=\dfrac12\cdot|AB|\cdot d_{P-AB}\\&=\dfrac{\sqrt2}{4}\cdot\sqrt{(8-m^2)m^2}\\&\leqslant\sqrt2.\end{split}\]当且仅当 $m=\pm2$ 时，等号成立．因此 $\triangle PAB$ 面积的最大值为 $\sqrt2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
