已知 $f(x)=x\ln x-\dfrac{k}{x}$ 的两个零点为 $x_1,x_2$，记 $f(x)$ 的导函数为 $f'(x)$，求证：$f'\left(\dfrac{x_1+x_2}2\right)\neq 0$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
将问题转化为证明 $x_1+x_2\neq 2x_0$ 后，考虑到$$f''(x)=\dfrac 1x-\dfrac{2k}{x^3},$$构造函数$$h(x)=f(x)-\left[\dfrac 12f''(x_0)(x-x_0)^2+f(x_0)\right],$$则其二阶导函数$$h''(x)=f''(x)-f''(x_0)=\dfrac 1x-\dfrac{2k}{x^3}-\dfrac{1}{x_0}+\dfrac{2k}{x_0^3}=\dfrac{(x-x_0)\left[2k(x^2+x_0x+x_0^2)-x_0^2x^2\right]}{x^3x_0^3}.$$考虑到 $k<0$，于是\[2k(x^2+x_0x+x_0^2)-x_0^2x^2<0,\]因此\[\begin{array} {c|ccc}\hline
x& (0,x_0)&x_0&(x_0,+\infty) \\ \hline
h''(x)&+&0&-\\ \hline
h'(x)&\nearrow &0&\searrow\\ \hline
h'(x)&- & 0 & -\\ \hline
h(x)&\searrow &0 &\searrow\\ \hline
h(x)&+&0&- \\ \hline
\end{array}\]如图．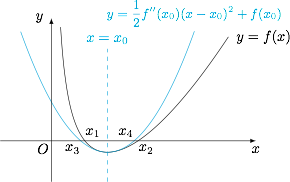
这样就有 $f(x)$ 的两个零点 $x_1,x_2$（$x_1<x_2$）和二次函数 $y=\dfrac 12f''(x_0)(x-x_0)^2+f(x_0)$ 的两个零点 $x_3,x_4$（$x_3<x_4$）满足$$x_3<x_1<x_4<x_2,$$进而$$x_1+x_2>x_3+x_4=2x_0,$$原命题得证．
x& (0,x_0)&x_0&(x_0,+\infty) \\ \hline
h''(x)&+&0&-\\ \hline
h'(x)&\nearrow &0&\searrow\\ \hline
h'(x)&- & 0 & -\\ \hline
h(x)&\searrow &0 &\searrow\\ \hline
h(x)&+&0&- \\ \hline
\end{array}\]如图．
这样就有 $f(x)$ 的两个零点 $x_1,x_2$（$x_1<x_2$）和二次函数 $y=\dfrac 12f''(x_0)(x-x_0)^2+f(x_0)$ 的两个零点 $x_3,x_4$（$x_3<x_4$）满足$$x_3<x_1<x_4<x_2,$$进而$$x_1+x_2>x_3+x_4=2x_0,$$原命题得证．
答案
解析
备注
