如图,在正方形 $ABCD$ 内,有五个边长是不同的整数的正方形,且它们的一条对角线都在 $AC$ 上,且 $AB$ 长是 $2015$,求这五个正方形的面积之和的最大值及最小值.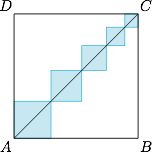

【难度】
【出处】
无
【标注】
【答案】
最小值为 $812055$,最大值为 $4020055$
【解析】
设这五个正方形的边长分别为 $x_1+1,x_2+2,x_3+3,x_4+4,x_5+5$,$x_i\in\mathbb N$,且 $x_1\leqslant x_2\leqslant x_3\leqslant x_4\leqslant x_5$,于是 $x_1+x_2+x_3+x_4+x_5=2000$.由于$$5\sum_{i=1}^na_i^2=(a_1+a_2+a_3+a_4+a_5)^2+\sum_{1\leqslant i<j\leqslant 5}(a_j-a_i)^2,$$于是\[\begin{split} 5\sum_{i=1}^5{(x_i+i)^2}=2015^2&+(x_2-x_1+1)^2+(x_3-x_1+2)^2+(x_4-x_1+3)^2+(x_5-x_1+4)^2\\ &+(x_3-x_2+1)^2+(x_4-x_2+2)^2+(x_5-x_2+3)^2\\ &+(x_4-x_3+1)^2+(x_5-x_3+2)^2+(x_5-x_4+1)^2,\end{split}\]显然当 $x_1=x_2=x_3=x_4=x_5=400$ 时取得最小值$$401^2+402^2+403^2+404^2+405^2=812055.$$另一方面,由于 $400\leqslant x_5\leqslant 2000$,有\[\begin{split} \sum_{i=1}^5{(x_i+i)^2}&=2015^2-2\big[(x_5+5)(x_1+x_2+x_3+x_4+10)+(x_4+4)(x_1+x_2+x_3+6)\\ &\qquad\qquad\qquad \qquad\qquad+(x_3+3)(x_1+x_2+3)+(x_2+2)(x_1+1)\big]\\ &=2015^2-2\big[(x_5+5)(2010-x_5)+(x_4+4)(x_1+x_2+x_3+6)\\&\qquad\qquad\qquad \qquad\qquad+(x_3+3)(x_1+x_2+3)+(x_2+2)(x_1+1)\big]\\ &\leqslant 2015^2-2\big[(2000+5)(2010-2000)+4\cdot 6+3\cdot 3+2\cdot 1\big],\end{split}\]等号当且仅当 $x_1=x_2=x_3=x_4=0$,$x_5=2000$ 时取得,因此所求的最大值为$$1^2+2^2+3^2+4^2+2005^2=4020055.$$
答案
解析
备注