如图，在长方体 $ ABCD-A_1B_1C_1D_1 $ 中，$ AB=AD=1$，$AA_1=2 $，$ M $ 为棱 $ DD_1 $ 上的一点．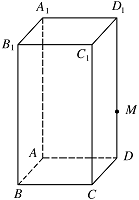
【难度】
【出处】
2012年高考福建卷（文）
【标注】
-
求三棱锥 $ A-MCC_1 $ 的体积；标注答案略解析由长方体 $ ABCD-A_1B_1C_1D_1 $ 知，$ AD\perp 平面 CDD_1C_1 $，
所以，点 $ A $ 到平面 $ CDD_1C_1 $ 的距离为 $ AD=1 $，又\[ S_{\triangle MCC_1}={\dfrac{1}{2}}CC_1\times CD={\dfrac{1}{2}}\times 2\times 1=1, \]所以\[ V_{A-MCC_1}={\dfrac{1}{3}}AD\cdot S_{\triangle MCC_1}={\dfrac{1}{3}}.\] -
当 $ A_1M+MC $ 取得最小值时，求证：$ B_1M\perp 平面 MAC $．标注答案略解析将侧面 $ CDD_1C_1 $ 绕 $ DD_1 $ 逆时针转 $ 90^\circ $ 展开，与侧面 $ ADD_1A_1 $ 共面（如图），
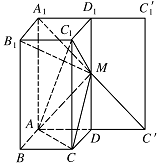当 $ A_1$，$M$，$C′ $ 共线时，$ A_1M+MC $ 取得最小值．
由 $ AD=CD=1$，$AA_1=2 $，得 $ M $ 为 $ DD_1 $ 中点．
连接 $ C_1M $，在 $ \triangle C_1MC $ 中，\[ MC_1={\sqrt{2}},MC={\sqrt{2}},CC_1=2 ,\]所以\[CC^2_1=MC^2_1+MC^2 ,\]得 $ \angle CMC_1=90^\circ $，即 $ CM\perp MC_1 $，
又由长方体 $ ABCD-A_1B_1C_1D_1 $ 知，$ B_1C_1\perp 平面 CDD_1C_1 $，
所以\[ B_1C_1\perp CM ,\]又\[B_1C_1\cap C_1M=C_1,\]所以\[CM\perp 平面 B_1C_1M ,\]得 $ CM\perp B_1M $；同理可证，$ B_1M\perp AM $，
又\[ AM\cap MC=M,\]所以 $B_1M\perp 平面 MAC $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
