如图,等边三角形 $ OAB $ 的边长为 $ 8{\sqrt{3}} $,且其三个顶点均在抛物线 $ E:x^2=2py\left(p>0\right) $ 上.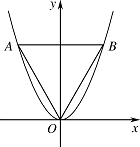

【难度】
【出处】
2012年高考福建卷(文)
【标注】
-
求抛物线 $ E $ 的方程;标注答案略解析依题意,得\[ |OB|=8{\sqrt{3}},\angle BOy=30^\circ .\]设 $ B\left(x,y\right) $,则\[\begin{split} x&=|OB|\sin 30^\circ =4{\sqrt{3}},\\y&=|OB|\cos 30^\circ =12. \end{split} \]因为点 $ B\left(4{\sqrt{3}},12\right) $ 在 $ x^2=2py $ 上,所以\[ \left(4{\sqrt{3}}\right)^2=2p\times 12, \]解得\[ p=2.\]故抛物线 $ E $ 的方程为\[ x^2=4y. \]
-
设动直线 $ l $ 与抛物线 $ E $ 相切于点 $ P $,与直线 $ y=-1 $ 相交于点 $ Q $.证明:以 $ PQ $ 为直径的圆恒过 $ y $ 轴上某定点.标注答案略解析由(1)知\[ y={\dfrac{1}{4}}x^2,y′={\dfrac{1}{2}}x .\]设 $ P\left(x_0,y_0\right) $,则 $ x_0\neq 0 $,且 $ l $ 的方程为\[ y-y_0={\dfrac{1}{2}}x_0\left(x-x_0\right), \]即\[ y={\dfrac{1}{2}}x_0x-{\dfrac{1}{4}}x^2_0. \]由\[ \begin{cases}y={\dfrac{1}{2}}x_0x-{\dfrac{1}{4}}x^2_0,\\y=-1.\end{cases} \]得\[\begin{cases}x ={\dfrac{x^2_0-4}{2x_0}},\\ y=-1. \end{cases}\]所以 $ Q $ 的坐标为\[\left( {\dfrac{x^2_0-4}{2x_0}},-1\right) .\]取 $ x_0=2 $,此时 $ P\left(2,1\right)$,$Q\left(0,-1\right) $,以 $ PQ $ 为直径的圆为\[ \left(x-1\right)^2+y^2=2 ,\]它与 $ y $ 轴交于点 $ M_1\left(0,1\right) $ 或 $ M_2\left(0,-1\right) $;
取 $ x_0=1 $,此时 $ P \left(1,{\dfrac{1}{4}}\right)$,$Q \left(-{\dfrac{3}{2}},-1\right) $,以 $ PQ $ 为直径的圆为\[ \left(x+{\dfrac{1}{4}} \right)^2+\left( y+{\dfrac{3}{8}} \right)^2={\dfrac{125}{64}}, \]它与 $ y $ 轴交于点 $ M_3\left(0,1\right) $ 或 $ M_4\left( 0,-{\dfrac{7}{4}}\right) $.
故若满足条件的点 $ M $ 存在,只能是 $ M\left(0,1\right) $.
以下证明点 $ M\left(0,1\right) $ 就是所要求的点.
因为\[ \overrightarrow {MP}=\left(x_0,y_0-1\right),\\ {\overrightarrow {MQ}}=\left( {\dfrac{x^2_0-4}{2x_0}},-2\right) ,\]所以\[\begin{split}{\overrightarrow {MP}}\cdot {\overrightarrow {MQ}}&={\dfrac{x^2_0-4}{2}}-2y_0+2\\&=2y_0-2-2y_0+2=0.\end{split} \]故以 $ PQ $ 为直径的圆恒过 $ y $ 轴上的定点 $ M \left(0,1\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2