已知圆 $O:x^2+y^2=4$，$F(0,2)$，点 $A,B$ 是圆 $O$ 上的动点，且 $|FA|\cdot |FB|=4$，是否存在与动直线 $AB$ 恒相切的定圆，若存在，求出该圆的方程；若不存在，请说明理由．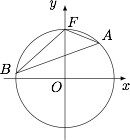
【难度】
【出处】
无
【标注】
【答案】
存在，圆的方程为 $x^2+(y-2)^2=1$
【解析】
如图．
设 $\angle AFB=\theta$，$FH\perp AB$ 于 $H$，则$$|AB|=2r\sin\dfrac {\angle AOB}2=4\sin\theta,$$其中 $r=2$ 为圆 $O$ 的半径，于是 $\triangle FAB$ 的面积$$S_{\triangle AFB}=\dfrac 12\cdot |AB|\cdot |FH|=2\sin\theta\cdot |FH|,$$同时亦有$$S_{\triangle AFB}=\dfrac 12\cdot \sin\theta\cdot |FA|\cdot |FB|=2\sin\theta,$$因此 $|FH|=1$ 为定值，于是定圆 $F:x^2+(y-2)^2=1$ 与动直线 $AB$ 恒相切．
设 $\angle AFB=\theta$，$FH\perp AB$ 于 $H$，则$$|AB|=2r\sin\dfrac {\angle AOB}2=4\sin\theta,$$其中 $r=2$ 为圆 $O$ 的半径，于是 $\triangle FAB$ 的面积$$S_{\triangle AFB}=\dfrac 12\cdot |AB|\cdot |FH|=2\sin\theta\cdot |FH|,$$同时亦有$$S_{\triangle AFB}=\dfrac 12\cdot \sin\theta\cdot |FA|\cdot |FB|=2\sin\theta,$$因此 $|FH|=1$ 为定值，于是定圆 $F:x^2+(y-2)^2=1$ 与动直线 $AB$ 恒相切．
答案
解析
备注
