如图，在长方体 $ ABCD-A_1B_1C_1D_1 $ 中，$ AA_1=AD=1$，$E $ 为 $ CD $ 的中点．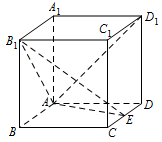
【难度】
【出处】
2012年高考福建卷（理）
【标注】
-
求证：$ B_1E\perp AD_1 $；标注答案略解析本题考查异面直线的垂直，可以利用向量法求解，也可以证明其中的一条直线 $AD_1$ 与 $B_1E$ 所在的平面 $A_1B_1ED$ 垂直．以 $ A $ 为原点，$ {\overrightarrow {AB}}$，${\overrightarrow {AD}}$，${\overrightarrow {AA_1}} $ 的方向分别为 $ x $ 轴，$ y $ 轴，$ z $ 轴的正方向建立空间直角坐标系（如图）．
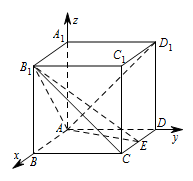设 $ AB=a $，则\[ A\left(0,0,0\right),D\left(0,1,0\right),D_1\left(0,1,1\right), E \left({\dfrac{a}{2}},1,0\right) ,B_1\left(a,0,1\right) ,\]故\[{\overrightarrow {AD_1}}=\left(0,1,1\right),{\overrightarrow {B_1E}}= \left(-{\dfrac{a}{2}},1,-1\right) , {\overrightarrow {AB_1}}=\left(a,0,1\right),{\overrightarrow {AE}}= \left({\dfrac{a}{2}},1,0 \right),\]因为\[{\overrightarrow {AD_1}}\cdot {\overrightarrow {B_1E}}=0,\]所以\[ B_1E\perp AD_1.\] -
在棱 $ AA_1 $ 上是否存在一点 $ P $，使得 $ DP\parallel 平面 B_1AE $？若存在，求 $ AP $ 的长；若不存在，请说明理由；标注答案存在点 $ P $，满足 $ DP\parallel 平面 B_1AE $，此时 $AP={\dfrac{1}{2}}$解析利用向量法进行求解即可．假设在棱 $ AA_1 $ 上存在一点 $ P\left(0,0,z_0\right) $，使得 $ DP\parallel 平面 B_1AE $．
此时 $ {\overrightarrow {DP}}=\left(0,-1,z_0\right) $．
设平面 $ B_1AE $ 的法向量 $\overrightarrow n=\left(x,y,z\right) $．
因为 $\overrightarrow n\perp 平面 B_1AE $，所以 $ \overrightarrow{n}\perp {\overrightarrow {AB_1}}$，$\overrightarrow{n}\perp {\overrightarrow {AE}}$，得\[ \begin{cases} ax+z=0 ,\\ {\dfrac{ax}{2}}+y=0.\end{cases} \]取 $ x=1 $，得平面 $ B_1AE $ 的一个法向量 $\overrightarrow n= \left(1,-{\dfrac{a}{2}},-a\right) $．
要使 $ DP\parallel 平面 B_1AE $，只要 $\overrightarrow n\perp {\overrightarrow {DP}} $，有 $ {\dfrac{a}{2}}-az_0=0 $，解得 $z_0={\dfrac{1}{2}}. $
又 $ DP\not\subset 平面 B_1AE $，所以存在点 $ P $，满足 $ DP\parallel 平面 B_1AE $，此时 $AP={\dfrac{1}{2}}$． -
若二面角 $ A-B_1E-A_1 $ 的大小为 $ 30^\circ $，求 $ AB $ 的长．标注答案$ 2 $解析利用向量法求解即可．连接 $ A_1D$，$B_1C $，由长方体 $ ABCD-A_1B_1C_1D_1 $ 及 $ AA_1=AD=1 $，得 $ AD_1\perp A_1D $．
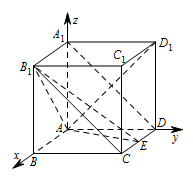因为 $ B_1C\parallel A_1D$，所以 $ AD_1\perp B_1C$．
又由（1）知 $ B_1E\perp AD_1 $，且 $ B_1C\cap B_1E=B_1 $，
所以 $ AD_1\perp 平面 DCB_1A_1 $，${\overrightarrow {AD_1}}$ 是平面 $ A_1B_1E $ 的一个法向量，此时 $ {\overrightarrow {AD_1}}=\left(0,1,1\right) $．
设 $ {\overrightarrow {AD_1}} $ 与 $\overrightarrow n $ 所成的角为 $ \theta $，则\[ \begin{split}\cos \theta &=\dfrac{\overrightarrow n\cdot {\overrightarrow {AD_1}}}{ \left |\overrightarrow n \right| \left|{\overrightarrow {AD_1}} \right|} \\&=\dfrac{{\dfrac{- a}{2}}-a}{ {\sqrt{2}}\cdot {\sqrt{1+{\dfrac{a^2}{4}}+a^2}} }.\end{split} \]因为二面角 $ A-B_1E-A_1 $ 的大小为 $ 30^\circ $，所以 $ |\cos \theta |=\cos 30^\circ$，即\[ \dfrac{{\dfrac{ 3a}{2}}}{{\sqrt{2}}\cdot {\sqrt{1+{\dfrac{5a^2}{4}}}}} ={\dfrac{{\sqrt{3}}}{2}},\]解得\[ a=2 ,\]即 $ AB $ 的长为 $ 2 $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
