如图,椭圆 $ E:{\dfrac{x^2}{a^2}}+{\dfrac{y^2}{b^2}}=1$ $\left(a>b>0\right) $ 的左焦点为 $ F_1 $,右焦点为 $ F_2 $,离心率 $ e={\dfrac{1}{2}} $,过 $ F_1 $ 的直线交椭圆于 $ A$,$B $ 两点,且 $ \triangle ABF_2 $ 的周长为 $ 8 $.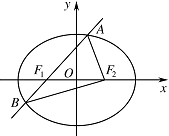

【难度】
【出处】
2012年高考福建卷(理)
【标注】
-
求椭圆 $ E $ 的方程;标注答案椭圆 $ E $ 的方程是\[ {\dfrac{x^2}{4}}+{\dfrac{y^2}{3}}=1. \]解析因为\[ |AB|+|AF_2|+|BF_2|=8 ,\]即\[ |AF_1|+|F_1B|+|AF_2|+|BF_2|=8, \]又\[ |AF_1|+|AF_2|=|BF_1|+|BF_2|=2a, \]所以\[ 4a=8,a=2. \]又因为 $ e={\dfrac{1}{2}} $,即 $ {\dfrac{c}{a}}={\dfrac{1}{2}} $,所以 $ c=1 $,所以\[ b={\sqrt{a^2-c^2}}={\sqrt{3}}. \]故椭圆 $ E $ 的方程是\[ {\dfrac{x^2}{4}}+{\dfrac{y^2}{3}}=1. \]
-
设动直线 $ l:y=kx+m $ 与椭圆 $ E $ 有且只有一个公共点 $ P $,且与直线 $ x=4 $ 相交于点 $ Q $.试探究:在坐标平面内是否存在定点 $ M $,使得以 $ PQ $ 为直径的圆恒过点 $ M $?若存在,求出点 $ M $ 的坐标;若不存在,请说明理由.标注答案存在定点 $ M\left(1,0\right) $,使得以 $ PQ $ 为直径的圆恒过点 $ M $,证明略解析由\[ \begin{cases}y=kx+m,\\ {\dfrac{x^2}{4}}+{\dfrac{y^2}{3}}=1, \end{cases} \]得\[ \left(4k^2+3\right)x^2+8kmx+4m^2-12=0 .\]因为动直线 $ l $ 与椭圆 $ E $ 有且只有一个公共点 $ P\left(x_0,y_0\right) $,
所以 $ m\neq 0 $ 且 $ \Delta =0 $,即\[ 64k^2m^2-4\left(4k^2+3\right)\left(4m^2-12\right)=0 ,\]化简得\[ 4k^2-m^2+3=0 . \]此时\[ \begin{split} x_0&=-{\dfrac{4km}{4k^2+3}}=-{\dfrac{4k}{m}}, \\ y_0&=kx_0+m={\dfrac{3}{m}},\end{split} \]所以 $ P \left(-{\dfrac{4k}{m}},{\dfrac{3}{m}} \right)$.
由 $ \begin{cases} x=4,\\ y=kx+m, \end{cases} $ 得 $ Q\left(4,4k+m\right) $.
假设平面内存在定点 $ M $ 满足条件,由图形对称性知,点 $ M $ 必在 $ x $ 轴上.
取 $ k=0$,$m={\sqrt{3}} $,此时 $ P\left(0, {\sqrt{3}}\right)$,$Q\left(4, {\sqrt{3}}\right) $,以 $ PQ $ 为直径的圆为\[\left(x-2\right)^2+\left(y-{\sqrt{3}}\right)^2=4 ,\]交 $ x $ 轴于点 $ M_1\left(1,0\right)$,$M_2\left(3,0\right) $;
取 $ k=-{\dfrac{1}{2}}$,$m=2 $,此时 $ P \left(1,{\dfrac{3}{2}}\right) $,$Q\left(4,0\right) $,以 $ PQ $ 为直径的圆为\[ \left( x-{\dfrac{5}{2}} \right)^2+ \left(y-{\dfrac{3}{4}} \right)^2={\dfrac{45}{16}} ,\]交 $ x $ 轴于点 $ M_3\left(1,0\right)$,$M_4\left(4,0\right) $.
所以若符合条件的点 $ M $ 存在,则 $ M $ 的坐标必为 $ \left(1,0\right) $.
以下证明 $ M\left(1,0\right) $ 就是满足条件的点:
因为 $ M $ 的坐标为 $ \left(1,0\right) $,所以\[ \begin{split} {\overrightarrow {MP}}&=\left( -{\dfrac{4k}{m}}-1,{\dfrac{3}{m}} \right),\\ {\overrightarrow {MQ}}&=\left(3,4k+m\right),\end{split} \]从而\[ \begin{split} {\overrightarrow {MP}}\cdot {\overrightarrow {MQ}}=-{\dfrac{12k }{m}}-3+{\dfrac{12k}{m}}+3=0,\end{split} \]故恒有 $ {\overrightarrow {MP}}\perp {\overrightarrow {MQ}} $,即存在定点 $ M\left(1,0\right) $,使得以 $ PQ $ 为直径的圆恒过点 $ M $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2