设 $ A $ 是单位圆 $ x^2+y^2=1 $ 上的任意一点，$ l $ 是过点 $ A $ 与 $ x $ 轴垂直的直线，$ D $ 是直线 $ l $ 与 $ x $ 轴的交点，点 $ M $ 在直线 $ l $ 上，且满足 $ |DM|=m|DA|\left(m>0且m\neq 1\right) $．当点 $ A $ 在圆上运动时，记点 $ M $ 的轨迹为曲线 $ C $．
【难度】
【出处】
2012年高考湖北卷（理）
【标注】
-
求曲线 $ C $ 的方程，判断曲线 $ C $ 为何种圆锥曲线，并求其焦点坐标；标注答案略解析如图 $ 1 $，
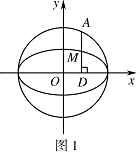设 $ M\left(x,y\right),A\left(x_0,y_0\right) $，则由\[ |DM|=m|DA|\left(m>0,且m\neq 1\right),\]可得\[ x=x_0,|y|=m|y_0|, \]所以\[ x_0=x,|y_0|={\dfrac{1}{m}}|y|, \quad \cdots \cdots ① \]因为 $ A $ 点在单位圆上运动，所以\[ x^2_0+y^2_0=1. \quad \cdots \cdots ② \]将 $ ① $ 式代入 $ ② $ 式即得所求曲线 $ C $ 的方程为\[ x^2+{\dfrac{y^2}{m^2}}=1\left(m>0,且m\neq 1\right).\]因为 $ m\in \left(0,1\right)\cup \left(1,+\infty \right) $，所以，
当 $ 0<m<1 $ 时，曲线 $ C $ 是焦点在 $ x $ 轴上的椭圆，两焦点坐标分别为\[ \left(-{\sqrt{1-m^2}},0\right),\left({\sqrt{1-m^2}},0\right) ,\]当 $ m>1 $ 时，曲线 $ C $ 是焦点在 $ y $ 轴上的椭圆，两焦点坐标分别为\[ \left(0,-{\sqrt{m^2-1}}\right),\left(0, {\sqrt{m^2-1}}\right) .\] -
过原点且斜率为 $ k $ 的直线交曲线 $ C $ 于 $ P,Q $ 两点，其中 $ P $ 在第一象限，它在 $ y $ 轴上的射影为点 $ N $，直线 $ QN $ 交曲线 $ C $ 于另一点 $ H $．是否存在 $ m $，使得对任意的 $ k>0 $，都有 $ PQ\perp PH $？若存在，求 $ m $ 的值；若不存在，请说明理由．标注答案略解析解法一：如图 $ 2 $、$ 3 $，
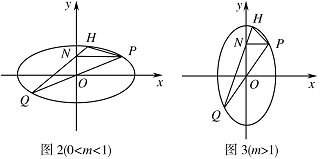$\forall k>0 $，设 $ P\left(x_1,kx_1\right),H\left(x_2,y_2\right),$ 则 $ Q\left(-x_1,-kx_1\right),N\left(0,kx_1\right)$，
直线 $ QN $ 的方程为\[ y=2kx+kx_1, \]将其代入椭圆 $ C $ 的方程并整理可得\[ \left(m^2+4k^2\right)x^2+4k^2x_1x+k^2x^2_1-m^2=0. \]依题意可知此方程的两根为 $ -x_1,x_2 $，于是由韦达定理可得\[ -x_1+x_2=-{\dfrac{4k^2x_1}{m^2+4k^2}}, \]即\[ x_2={\dfrac{m^2x_1}{m^2+4k^2}}.\]因为点 $ H $ 在直线 $ QN $ 上，所以\[ y_2-kx_1=2kx_2={\dfrac{2km^2x_1}{m^2+4k^2}}. \]于是\[\begin{split} \overrightarrow {PQ}&=\left(-2x_1,-2kx_1\right),\\ \overrightarrow {PH} &=\left(x_2-x_1,y_2-kx_1\right)\\&= \left(-\dfrac{4k^2x_1}{m^2+4k^2},\dfrac{2km^2x_1}{m^2+4k^2} \right). \end{split}\]而 $ PQ\perp PH $ 等价于\[ {\overrightarrow {PQ}}\cdot {\overrightarrow {PH}}={\dfrac{4\left(2-m^2\right)k^2x^2_1}{m^2+4k^2}}=0, \]即 $ 2-m^2=0 $，又 $ m>0 $，得\[ m={\sqrt{2}},\]故存在 $ m={\sqrt{2}} $，使得在其对应的椭圆 $ x^2+{\dfrac{y^2}{2}}= 1$ 上，
对任意的 $ k>0 $，都有 $ PQ\perp PH $．
解法二：如图 $ 2,3 $，$ x_1\in \left(0,1\right) $，设 $ P\left(x_1,y_1\right),H\left(x_2,y_2\right) $，
则 $ Q\left(-x_1,-y_1\right),N\left(0,y_1\right) $．因为 $ P ,H$ 两点在椭圆 $ C $ 上，所以\[ \begin{cases}m^2x^2_1+y^2_1=m^2,\\m^2x^2_2+y^2_2=m^2,\end{cases}\]两式相减可得\[ m^2\left(x^2_1-x^2_2\right)+\left(y^2_1-y^2_2\right)=0, \quad \cdots \cdots ③ \]依题意，由点 $ P $ 在第一象限可知，点 $ H $ 也在第一象限，且 $ P,H $ 不重合，故\[ \left(x_1-x_2\right)\left(x_1+x_2\right)\neq 0. \]于是由 $ ③ $ 式可得\[ {\dfrac{\left(y_1-y_2\right)\left(y_1+y_2\right)}{\left(x_1-x_2\right)\left(x_1+x_2\right)}}=-m^2. \quad \cdots \cdots ④ \]又 $ Q,N,H $ 三点共线，所以 $ k_{QN}=k_{QH }$，即\[ {\dfrac{2y_1}{x_1}}={\dfrac{y_1+y_2}{x_1+x_2}}. \]于是由 $ ④ $ 式可得\[\begin{split} k_{PQ}\cdot k_{PH} &=\dfrac{y_1}{x_1}\cdot \dfrac{y_1-y_2}{x_1-x_2}\\&=\dfrac{1}{2}\cdot \dfrac{\left(y_1-y_2\right)\left(y_1+y_2\right)}{\left(x_1-x_2\right)\left(x_1+x_2\right)}\\&=-\dfrac{m^2}{2}.\end{split} \]而 $ PQ\perp PH $ 等价于 $ k_{PQ}\cdot k_{PH}=-1 $，即\[ -{\dfrac{m^2}{2}}=-1 ,\]又 $ m>0 $，得\[ m={\sqrt{2}}, \]故存在 $ m={\sqrt{2}} $，使得在其对应的椭圆 $ x^2+{\dfrac{y^2}{2}}=1 $ 上，
对任意的 $ k>0 $，都有 $ PQ\perp PH $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
