如图,在四棱锥 $ P-ABCD $ 中,$ PA\perp $ 平面 $ ABCD$,$AB=4$,$BC=3$,$AD=5$,$\angle DAB=\angle ABC=90^\circ$,$E $ 是 $ CD $ 的中点.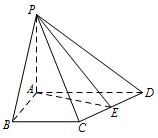

【难度】
【出处】
2012年高考湖南卷(理)
【标注】
-
证明:$ CD\perp $ 平面 $ PAE $;标注答案略解析解法一:如图,连接 $ AC $.
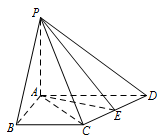 由 $ AB=4,BC=3,\angle ABC=90^\circ $,得 $ AC=5$.又 $AD=5$,$ E $ 是 $ CD $ 的中点,所以\[ CD\perp AE. \]因为 $ PA\perp $ 平面 $ ABCD $,$ CD $ $ \subset $ 平面 $ ABCD $,所以\[ PA\perp CD. \]而 $ PA,AE $ 是平面 $ PAE $ 内的两条相交直线,所以\[ CD\perp 平面 PAE .\]解法二:如图,
由 $ AB=4,BC=3,\angle ABC=90^\circ $,得 $ AC=5$.又 $AD=5$,$ E $ 是 $ CD $ 的中点,所以\[ CD\perp AE. \]因为 $ PA\perp $ 平面 $ ABCD $,$ CD $ $ \subset $ 平面 $ ABCD $,所以\[ PA\perp CD. \]而 $ PA,AE $ 是平面 $ PAE $ 内的两条相交直线,所以\[ CD\perp 平面 PAE .\]解法二:如图,
以 $ A $ 为坐标原点,$AB,AD,AP$ 所在直线分别为 $x$ 轴,$y$ 轴,$z$ 轴建立空间直角坐标系.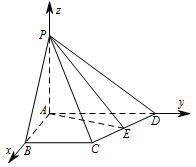 设 $PA=h$,则相关各点的坐标为\[ A\left(0,0,0\right),B\left(4,0,0\right),C\left(4,3,0\right),D\left(0,5,0\right),E\left(2,4,0\right),P\left(0,0,h\right). \]易知\[ \begin{split}\overrightarrow {CD} &=\left(-4,2,0\right), \overrightarrow {AE}&=\left(2,4,0\right), \overrightarrow {AP} &=\left(0,0,h\right).\end{split} \]因为\[ \begin{split} \overrightarrow {CD}\cdot \overrightarrow {AE} &=-8+8+0=0,\\ \overrightarrow {CD} \cdot \overrightarrow {AP} &=0, \end{split}\]所以\[ CD\perp AE,CD\perp AP. \]而 $ AP,AE $ 是平面 $ PAE $ 内的两条相交直线,所以\[ CD\perp 平面PAE .\]
设 $PA=h$,则相关各点的坐标为\[ A\left(0,0,0\right),B\left(4,0,0\right),C\left(4,3,0\right),D\left(0,5,0\right),E\left(2,4,0\right),P\left(0,0,h\right). \]易知\[ \begin{split}\overrightarrow {CD} &=\left(-4,2,0\right), \overrightarrow {AE}&=\left(2,4,0\right), \overrightarrow {AP} &=\left(0,0,h\right).\end{split} \]因为\[ \begin{split} \overrightarrow {CD}\cdot \overrightarrow {AE} &=-8+8+0=0,\\ \overrightarrow {CD} \cdot \overrightarrow {AP} &=0, \end{split}\]所以\[ CD\perp AE,CD\perp AP. \]而 $ AP,AE $ 是平面 $ PAE $ 内的两条相交直线,所以\[ CD\perp 平面PAE .\] -
若直线 $ PB $ 与平面 $ PAE $ 所成的角和 $ PB $ 与平面 $ ABCD $ 所成的角相等,求四棱锥 $ P-ABCD $ 的体积.标注答案略解析法一:在 $AD$ 上取 $DG=BC=3$,连接 $BG$ 交 $AE$ 于点 $F$,连接 $PF$,如图:
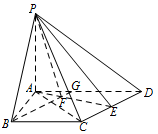 四边形 $BCDF$ 为平行四边形,从而 $BG\parallel CD$.
四边形 $BCDF$ 为平行四边形,从而 $BG\parallel CD$.
由(1)知 $BG\perp 平面PAE$,所以 $\angle BPF$ 即为 $PB$ 与平面 $PAE$ 所成的角.
而 $\angle PBA$ 为 $PB$ 与平面 $ABCD$ 所成的角,所以 $\angle BPF=\angle PBA$.
$\sin\angle PBA=\dfrac{PA}{PB}=\sin \angle BPF=\dfrac{BF}{PB}$,所以 $PA=BF$.
而 $\sin\angle BAF=\dfrac{BF}{BA}=\sin D=\dfrac{4}{\sqrt{4^2+2^2}}=\dfrac{BF}{4}$,
解得 $PA=BF=\dfrac{8\sqrt 5}{5}$.
所以四棱锥 $ P-ABCD $ 的体积为\[ \begin{split}V&={\dfrac{1}{3}}\times \dfrac 12\times\left(3+5\right)\times 4\times {\dfrac{8{\sqrt{5}}}{5}}={\dfrac{128{\sqrt{5}}}{15}}.\end{split} \]法二:由题设和(1)知,$ {\overrightarrow {CD}},{\overrightarrow {PA}} $ 分别是平面 $ PAE $,平面 $ ABCD $ 的法向量.
而 $ PB $ 与平面 $ PAE $ 所成的角和 $ PB $ 与平面 $ ABCD $ 所成的角相等,所以\[ \left |\cos \left \langle \overrightarrow {CD},\overrightarrow {PB} \right \rangle \right|= \left|\cos \left \langle \overrightarrow {PA}, \overrightarrow {PB} \right \rangle \right|, \]即\[ \left|{\dfrac{{\overrightarrow {CD}}\cdot {\overrightarrow {PB}}}{|{\overrightarrow {CD}}|\cdot |{\overrightarrow {PB}}|}} \right |= \left| {\dfrac{{\overrightarrow {PA}}\cdot {\overrightarrow {PB}}}{|{\overrightarrow {PA}}|\cdot |{\overrightarrow {PB}}|}} \right|.\]由(1)知,\[ {\overrightarrow {CD}}=\left(-4,2,0\right),{\overrightarrow {PA}}=\left(0,0,-h\right) ,\]又 $ {\overrightarrow {PB}}=\left(4,0,-h\right) $,故\[ \left| {\dfrac{-16+0+0}{2{\sqrt{5}}\cdot {\sqrt{16+h^2}}}} \right|=\left| {\dfrac{0+0+h^2}{h\cdot {\sqrt{16+h^2}}}} \right|, \]解得 $ h={\dfrac{8{\sqrt{5}}}{5}} $.又梯形 $ ABCD $ 的面积为\[ S={\dfrac{1}{2}}\times \left(5+3\right)\times 4=16, \]所以四棱锥 $ P-ABCD $ 的体积为\[ \begin{split}V&={\dfrac{1}{3}}\times S\times PA={\dfrac{1}{3}}\times 16\times {\dfrac{8{\sqrt{5}}}{5}}={\dfrac{128{\sqrt{5}}}{15}}.\end{split} \]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2