已知函数 $ f\left(x\right)=A\sin \left(\omega x+\varphi \right)\left( x\in {\mathbb{R}},\omega >0,0<\varphi <{\dfrac{{\mathrm \pi } }{2}}\right) $ 的部分图象如图所示.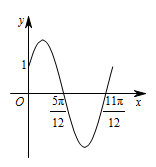

【难度】
【出处】
2012年高考湖南卷(文)
【标注】
-
求函数 $ f\left(x\right) $ 的解析式;标注答案略解析由题设图象知,周期\[ T=2 \left({\dfrac{11{\mathrm \pi } }{12}}-{\dfrac{5{\mathrm \pi } }{12}}\right) ={\mathrm \pi }, \]所以\[\omega ={\dfrac{2{\mathrm \pi }}{T}}=2.\]因为点 $ \left({\dfrac{5\mathrm \pi }{12}},0\right) $ 在函数图象上,所以\[ A\sin \left(2\times {\dfrac{5{\mathrm \pi } }{12}}+\varphi \right)=0, \]即\[ \sin \left( {\dfrac{5{\mathrm \pi } }{6}}+\varphi \right)=0, \]又因为 $ 0<\varphi <{\dfrac{\mathrm \pi }{2}} $,所以\[ {\dfrac{5{\mathrm \pi } }{6}}<{\dfrac{5{\mathrm \pi }}{6}}+\varphi <{\dfrac{4{\mathrm \pi } }{3}},\]从而\[{\dfrac{5{\mathrm \pi }}{6}}+\varphi ={\mathrm \pi } , \]解得\[\varphi ={\dfrac{{\mathrm \pi } }{6}}.\]又点 $ \left(0,1\right) $ 在函数图象上,所以\[ A\sin {\dfrac{\mathrm \pi }{6}}=1, \]解得\[A=2.\]故函数 $ f\left(x\right) $ 的解析式为\[ f\left(x\right)=2\sin \left(2x+{\dfrac{{\mathrm \pi } }{6}}\right) . \]
-
求函数 $ g\left(x\right)=f\left( x-{\dfrac{\mathrm \pi }{12}}\right) -f\left( x+{\dfrac{\mathrm \pi }{12}}\right) $ 的单调递增区间.标注答案略解析\[\begin{split} g\left(x\right) &=2\sin \left[2 \left(x-{\dfrac{\mathrm \pi }{12}}\right) +{\dfrac{{\mathrm \pi } }{6}} \right]-2\sin \left[ 2\left( x+{\dfrac{{\mathrm \pi } }{12}}\right) +{\dfrac{{\mathrm \pi } }{6}}\right] \\&=2\sin 2x-2\sin \left(2x+{\dfrac{{\mathrm \pi } }{3}}\right) \\&=2\sin 2x-2 \left({\dfrac{1}{2}}\sin 2x+{\dfrac{{\sqrt{3}}}{2}}\cos 2x \right)\\&=\sin 2x-{\sqrt{3}}\cos 2x\\&=2\sin \left(2x-{\dfrac{\mathrm \pi }{3}}\right) .\end{split} \]由 $ 2k{\mathrm \pi } -{\dfrac{{\mathrm \pi } }{2}}\leqslant 2x-{\dfrac{{\mathrm \pi } }{3}}\leqslant 2k{\mathrm \pi }+{\dfrac{{\mathrm \pi } }{2}} $,得\[ k{\mathrm \pi } -{\dfrac{{\mathrm \pi } }{12}}\leqslant x\leqslant k{\mathrm \pi } +{\dfrac{5{\mathrm \pi }}{12}},k\in {\mathbb{Z}}. \]所以函数 $ g\left(x\right) $ 的单调递增区间是\[ \left[k{\mathrm \pi } -{\dfrac{{\mathrm \pi } }{12}},k{\mathrm \pi } +{\dfrac{5{\mathrm \pi } }{12}}\right] ,k\in {\mathbb{Z}}. \]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2