如图,在四棱锥 $ P-ABCD $ 中,$ PA\perp $ 平面 $ ABCD $,底面 $ ABCD $ 是等腰梯形,$ AD\parallel BC$,$AC\perp BD $.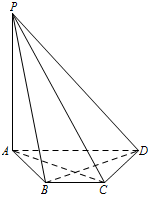

【难度】
【出处】
2012年高考湖南卷(文)
【标注】
-
证明:$ BD\perp PC $;标注答案略解析因为 $ PA\perp $ 平面 $ ABCD $,$ BD \subset $ 平面 $ ABCD $,
所以 $ PA\perp BD $.
又 $ AC\perp BD$,$PA,AC $ 是平面 $ PAC $ 内的两条相交直线,
所以 $ BD\perp $ 平面 $ PAC $.
而 $ PC \subset $ 平面 $ PAC $,所以 $ BD\perp PC $. -
若 $ AD=4$,$BC=2 $,直线 $ PD $ 与平面 $ PAC $ 所成的角为 $ 30^\circ $,求四棱锥 $ P-ABCD $ 的体积.标注答案略解析如图:
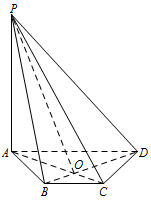 设 $ AC $ 和 $ BD $ 相交于点 $ O $,连接 $ PO $,
设 $ AC $ 和 $ BD $ 相交于点 $ O $,连接 $ PO $,
由(1)知,$ BD\perp $ 平面 $ PAC $,所以 $ \angle DPO $ 是直线 $ PD $ 和平面 $ PAC $ 所成的角.
从而 $ \angle DPO=30^\circ $.
由 $ BD\perp $ 平面 $ PAC$,$PO\subset $ 平面 $ PAC $ 知,$ BD\perp PO $.
在 $ {\mathrm{Rt}}\triangle POD $ 中,由 $ \angle DPO=30^\circ $ 得 $ PD=2OD $.
因为四边形 $ ABCD $ 为等腰梯形,$ AC\perp BD $,
所以 $ \triangle AOD$,$\triangle BOC $ 均为等腰直角三角形.从而梯形 $ ABCD $ 的高为\[ {\dfrac{1}{2}}AD+{\dfrac{1}{2}}BC={\dfrac{1}{2}}\times \left(4+2\right)=3 ,\]于是梯形 $ ABCD $ 的面积\[ S={\dfrac{1}{2}}\times \left(4+2\right)\times 3=9, \]在等腰直角三角形 $ AOD $ 中,\[ OD={\dfrac{{\sqrt{2}}}{2}}AD=2{\sqrt{2}}, \]所以\[\begin{split} PD&=2OD=4{\sqrt{2}},\\PA&={\sqrt{PD^2-AD^2}}=4.\end{split}\]故四棱锥 $ P-ABCD $ 的体积为\[\begin{split}V&={\dfrac{1}{3}}\times S\times PA\\&={\dfrac{1}{3}}\times 9\times 4\\&=12.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2