$ a=0 $，$ b=-3 $

由题设知\[ f '\left(x\right)=3x^2+2ax+b, \]且\[ \begin{split} f '\left(-1\right)&=3-2a+b=0,\\f ′\left(1\right)&=3+2a+b=0, \end{split} \]解得\[ a=0,b=-3. \]

$ g\left(x\right) $ 的极值点为 $ -2 $

由（1）知\[f\left(x\right)=x^3-3x .\]因为 $ f\left(x\right)+2=\left(x-1\right)^2\left(x+2\right) $，所以 $ g'\left(x\right)=0 $ 的根为\[ x_1=x_2=1,x_3=-2 ,\]于是函数 $ g\left(x\right) $ 的极值点只可能是 $ 1 $ 或 $ -2 $．
当 $ x<-2 $ 时，$ g'\left(x\right)<0 $；
当 $ -2<x<1 $ 时，$ g'\left(x\right)>0 $，故 $ -2 $ 是 $ g\left(x\right) $ 的极值点．
当 $ -2<x<1 $ 或 $ x>1 $ 时，$ g'\left(x\right)>0 $，故 $ 1 $ 不是 $ g\left(x\right) $ 的极值点．
所以 $ g\left(x\right) $ 的极值点为 $ -2 $．

当 $ |c|=2 $ 时，函数 $ y=h\left(x\right) $ 有 $ 5 $ 个零点；当 $ |c|<2 $ 时，函数 $ y=h\left(x\right) $ 有 $ 9 $ 个零点

令 $ f\left(x\right)=t $，则\[ h\left(x\right)=f\left(t\right)-c .\]先讨论关于 $ x $ 的方程 $ f\left(x\right)=c $ 根的情况，$ c\in \left[-2,2\right] $．
由（1）知\[ f ′\left(x\right)=3\left(x+1\right)\left(x-1\right) .\]所以 $f\left(x\right)$ 在 $\left(-\infty,-1\right)$ 与 $\left(1,+\infty\right)$ 上单调递增，在 $\left(-1,1\right)$ 上单调递减；又由（2）知，$ f\left(x\right)=-2 $ 有两个不同的根为 $ 1 $ 和 $ -2 $，注意到 $ f\left(x\right) $ 是奇函数，得到 $f\left(x\right)$ 的草图如下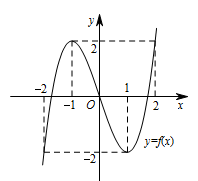： 于是，当 $ |c|=2 $ 时，$ f\left(x\right)=c $ 有两个不同的根 $ x_1$，$x_2 $ 满足 $ |x_1|=1$，$|x_2|=2 $；
当 $ |c|<2 $ 时，$ f\left(x\right)=c $ 有三个不同的根 $ x_3$，$x_4$，$x_5 $ 满足 $|x_i|<2,i=3,4,5$．
结合考虑 $f\left(x\right)=x_i,i=1,2,3,4,5$ 的零点我们得到 $y=h\left(x\right)$ 的零点：
（i）当 $ |c|=2 $ 时，$ f\left(t\right)=c $ 有两个根 $ t_1$，$t_2 $ 满足 $ |t_1|=1$，$|t_2|=2 $，而 $ f\left(x\right)=t_1 $ 有三个不同的根，$ f\left(x\right)=t_2 $ 有两个不同的根，故 $ y=h\left(x\right) $ 有 $ 5 $ 个零点．
（ii）当 $ |c|<2 $ 时，$ f\left(t\right)=c $ 有三个不同的根 $ t_3$，$t_4$，$t_5 $ 满足 $ |t_i|<2,i=3,4,5 $，而 $ f\left(x\right)=t_i\left(i=3,4,5\right) $ 各有三个不同的根，故 $ y=h\left(x\right) $ 有 $ 9 $ 个零点．
综上可知，
当 $ |c|=2 $ 时，函数 $ y=h\left(x\right) $ 有 $ 5 $ 个零点；当 $ |c|<2 $ 时，函数 $ y=h\left(x\right) $ 有 $ 9 $ 个零点．