如图,$ AB $ 是圆 $ O $ 的直径,$ D $,$ E $ 为圆上位于 $ AB $ 异侧的两点,连接 $ BD $ 并延长至点 $ C $,使 $ BD = DC $,连接 $ AC $,$ AE $,$ DE $.求证:$\angle E = \angle C$.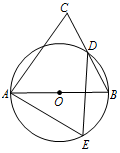

【难度】
【出处】
2012年高考江苏卷
【标注】
-
标注答案略解析连接 $ OD $,因为 $ BD=DC $,$ O $ 为 $ AB $ 的中点,
所以 $ OD\parallel AC $,于是 $ \angle ODB=\angle C $.
因为 $ OB=OD $,所以 $ \angle ODB=\angle B $.
于是 $ \angle B=\angle C $.因为点 $ A $,$ E $,$ B $,$ D $ 都在圆 $ O $ 上,且 $ D $,$ E $ 为圆 $ O $ 上位于 $ AB $ 异侧的两点,所以 $ \angle E $ 和 $ \angle B $ 为同弧所对的圆周角,故 $ \angle E=\angle B $.所以 $ \angle E=\angle C $.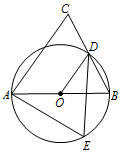
题目
问题1
答案1
解析1
备注1