如图,从 $ A_1\left(1,0,0\right),A_2\left(2,0,0\right),B_1\left(0,1,0\right), B_2\left(0,2,0\right),C_1\left(0,0,1\right),C_2\left(0,0,2\right) $ 这 $ 6 $ 个点中随机选取 $ 3 $ 个点,将这 $ 3 $ 个点及原点 $ O $ 两两相连构成一个"立体",记该"立体"的体积为随机变量 $ V $(如果选取的 $ 3 $ 个点与原点在同一个平面内,此时"立体"的体积 $ V=0 $).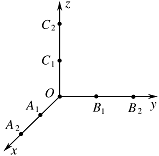

【难度】
【出处】
2012年高考江西卷(理)
【标注】
-
求 $ V=0 $ 的概率;标注答案略解析从 $ 6 $ 个点中随机选取 $ 3 $ 个点总共有 $ {\mathrm{C}}^3_6=20 $ 种取法,
选取的 $ 3 $ 个点与原点在同一个平面内的取法有 ${\mathrm{ C}}^1_3{\mathrm C}^3_4=12 $ 种,
因此 $ V=0 $ 的概率为 $ P\left(V=0\right)={\dfrac{12}{20}}={\dfrac{3}{5}} $. -
求 $ V $ 的分布列及数学期望 $ EV $.标注答案略解析$ V $ 的所有可能取值为 $ 0 ,{\dfrac{1}{6}},{\dfrac{1}{3}},{\dfrac{2}{3}},{\dfrac{4}{3}} $,因此 $ V $ 的分布列为\begin{array}{|c|c|c|c|c|c|c|} \hline
V &0 &{\dfrac{1}{6}} &{\dfrac{1}{3}}& {\dfrac{2}{3}} &{\dfrac{4}{3}} \\ \hline
P &{\dfrac{3}{5}} &{\dfrac{1}{20}}& {\dfrac{3}{20}}& {\dfrac{3}{20}}& {\dfrac{1}{20}} \\ \hline
\end{array}由 $ V $ 的分布列可得\[ \begin{split}EV&=0\times {\dfrac{3}{5}}+{\dfrac{1}{6}}\times {\dfrac{1}{20}}+{\dfrac{1}{3}}\times {\dfrac{3}{20}}+{\dfrac{2}{3}}\times {\dfrac{3}{20}}+{\dfrac{4}{3}}\times {\dfrac{1}{20}}\\&={\dfrac{9}{40}} .\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2