题目 函数 $f(x)=ax^3+3x^2+3x$（$a\ne 0$）． 问题1 讨论 $f(x)$ 的单调性； 答案1 记 $\alpha=\dfrac{-1+\sqrt{1-a}}{a}$，$\beta=\dfrac{-1-\sqrt{1-a}}{a}$．<br/>当 $a<0$ 时函数 $f(x)$ 在 $\left(-\infty ,\alpha\right)$ 上单调递减，在 $\left(\alpha,\beta\right)$ 上单调递增，在 $\left(\beta,+\infty \right)$ 上单调递减；当 $0<a<1$ 时，函数 $f(x)$ 在 $\left(-\infty,\beta\right)$ 上单调递增，在 $\left(\beta,\alpha\right)$ 上单调递减，在 $\left(\alpha,+\infty \right)$ 上单调递增；当 $a\geqslant 1$ 时，函数 $f(x)$ 在 $\mathbb R$ 上单调递增 解析1 函数 $f(x)$ 的导函数$$f'(x)=3(ax^2+2x+1),$$设函数 $h(x)=ax^2+2x+1$，则其对称轴为 $x=-\dfrac 1a$，判别式 $\Delta=4(1-a)$，因此按 $a$ 与 $0,1$ 的大小关系展开讨论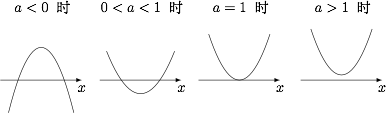．<img src="/static/images/3e0b9fc2efecbe7c8a4e412a2e6789a2.png" class="img-responsive" />记 $\alpha=\dfrac{-1+\sqrt{1-a}}{a}$，$\beta=\dfrac{-1-\sqrt{1-a}}{a}$．<br/><case>情形一</case> $a<0$．<br/>函数 $f(x)$ 在 $\left(-\infty ,\alpha\right)$ 上单调递减，在 $\left(\alpha,\beta\right)$ 上单调递增，在 $\left(\beta,+\infty \right)$ 上单调递减；<br/><case>情形二</case> $0<a<1$．<br/>函数 $f(x)$ 在 $\left(-\infty,\beta\right)$ 上单调递增，在 $\left(\beta,\alpha\right)$ 上单调递减，在 $\left(\alpha,+\infty \right)$ 上单调递增；<br/><case>情形三</case> $a\geqslant 1$．<br/>函数 $f(x)$ 在 $\mathbb R$ 上单调递增． 备注1 问题2 若 $f(x)$ 在区间 $(1,2)$ 是增函数，求 $a$ 的取值范围． 答案2 $\left[-\dfrac 54,0\right)\cup (0,+\infty )$ 解析2 题意即\[\forall x\in (1,2),3(ax^2+2x+1)\geqslant 0,\]即$$\forall x\in (1,2),a\geqslant -\dfrac{2x+1}{x^2},$$令 $t=\dfrac 1x$，则问题等价于$$\forall t\in\left(\dfrac 12,1\right),a\geqslant -t^2-2t,$$由于函数 $y=-t^2-2t$ 在区间 $\left(\dfrac 12,1\right)$ 上的取值范围是 $\left(-3,-\dfrac 54\right)$，因此 $a$ 的取值范围是 $\left[-\dfrac 54,0\right)\cup (0,+\infty )$． 备注2