在三棱柱 $ ABC-A_1B_1C_1 $ 中，已知 $ AB=AC=AA_1={\sqrt{5}}$，$BC=4 $，点 $ A_1 $ 在底面 $ ABC $ 的射影是线段 $ BC $ 的中点 $ O $．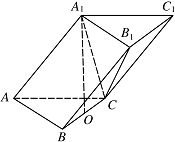
【难度】
【出处】
2012年高考江西卷（理）
【标注】
-
证明：在侧棱 $ AA_1 $ 上存在一点 $ E $，使得 $ OE\perp 平面 BB_1C_1C $，并求出 $ AE $ 的长；标注答案略解析连接 $ AO $，在 $ \triangle AOA_1 $ 中，作 $ OE\perp AA_1 $ 于点 $ E $．
因为 $ AA_1\parallel BB_1 $，所以 $ OE\perp BB_1 $，
因为 $ A_1O\perp 平面 ABC $，所以 $ A_1O\perp BC $．
因为 $ AB=AC$，$OB=OC $，所以 $ AO\perp BC $，
所以 $ BC\perp 平面 AA_1O $，所以 $ BC\perp OE $，
所以 $ OE\perp 平面 BB_1C_1C $．
在 $ {\mathrm{Rt}}\triangle AOB$ 中，\[ AO={\sqrt{AB^2-BO^2}}=1, \]由 $AA_1={\sqrt{5}}$ 及射影定理，得\[ AE={\dfrac{AO^2}{AA_1}}={\dfrac{{\sqrt{5}}}{5}} .\] -
求平面 $ A_1B_1C $ 与平面 $ BB_1C_1C $ 夹角的余弦值．标注答案略解析如图，
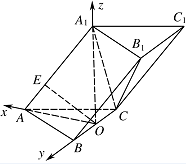分别以 $ OA$、$OB$、$OA_1 $ 所在直线为 $ x$、$y$、$z $ 轴，建立空间直角坐标系，则\[A\left(1,0,0\right),B\left(0,2,0\right),C\left(0,-2,0\right),A_1\left(0,0,2\right) ,\]由 $ {\overrightarrow {AE}}={\dfrac{1}{5}}{\overrightarrow {AA_1}} $，得点 $ E $ 的坐标是\[ \left({\dfrac{4}{5}},0,{\dfrac{2}{5}} \right) ,\]由（1）得平面 $ BB_1C_1C $ 的法向量是\[ {\overrightarrow {OE}}= \left({\dfrac{4}{5}},0,{\dfrac{2}{5}}\right) .\]设平面 $ A_1B_1C $ 的法向量为 $\overrightarrow n=\left(x,y,z\right) $，由\[ \begin{cases}\overrightarrow n\cdot {\overrightarrow {A_1B_1}}=0,\\ \overrightarrow n\cdot {\overrightarrow {A_1C}}=0 ,\end{cases}\]得\[\begin{cases}-x+2y=0,\\y+z=0 ,\end{cases}\]令 $ y=1 $，得\[\overrightarrow n=\left(2,1,-1\right) ,\]所以\[ \cos \left \langle\overrightarrow {OE},\overrightarrow n \right \rangle= \dfrac{{\overrightarrow {OE}}\cdot \overrightarrow n}{\left |{\overrightarrow {OE}}\right |\cdot \left |\overrightarrow n\right| }={\dfrac{{\sqrt{30}}}{10}} ,\]即平面 $ BB_1C_1C $ 与平面 $ A_1B_1C $ 的夹角的余弦值是 $ {\dfrac{{\sqrt{30}}}{10}} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
