查看数据源：599165b62bfec200011de1eb
如图，从 $ A_1\left(1,0,0\right)$，$A_2\left(2,0,0\right)$，$B_1\left(0,1,0\right)$，$B_2\left(0,2,0\right)$，$ C_1\left(0,0,1\right)$，$C_2\left(0,0,2\right) $ 这 $ 6 $ 个点中随机选取 $ 3 $ 个点．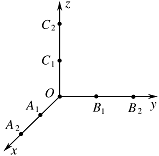 
【难度】
【出处】
2012年高考江西卷（文）
【标注】
  1. 求这 $ 3 $ 点与原点 $ O $ 恰好是正三棱锥的四个顶点的概率；
    标注
    答案
    略
    解析
    从这 $ 6 $ 个点中随机选取 $ 3 $ 个点的所有可能结果是：
    $ x $ 轴上取 $ 2 $ 个点的有 $ A_1A_2B_1$，$A_1A_2B_2$，$A_1A_2C_1$，$A_1A_2C_2 $ 共 $ 4 $ 种；
    $ y $ 轴上取 $ 2 $ 个点的有 $ B_1B_2A_1$，$B_1B_2A_2$，$B_1B_2C_1$，$B_1B_2C_2 $ 共 $ 4 $ 种；
    $ z $ 轴上取 $ 2 $ 个点的有 $ C_1C_2A_1$，$C_1C_2A_2$，$C_1C_2B_1$，$C_1C_2B_2 $ 共 $ 4 $ 种；
    所选取的 $ 3 $ 个点在不同坐标轴上有 $ A_1B_1C_1$，$A_1B_1C_2$，$A_1B_2C_1$，$A_1B_2C_2$，$A_2B_1C_1$，$A_2B_1C_2$，$A_2B_2C_1$，$A_2B_2C_2 $ 共 $ 8 $ 种．
    因此，从这 $ 6 $ 个点中随机选取 $ 3 $ 个点的所有可能结果共 $ 20 $ 种．
    选取的这 $ 3 $ 个点与原点 $ O $ 恰好是正三棱锥的四个顶点的所有可能结果有 $ A_1B_1C_1$，$A_2B_2C_2 $ 共 $ 2 $ 种，
    因此，这 $ 3 $ 个点与原点 $ O $ 恰好是正三棱锥的四个顶点的概率为\[ P_1={\dfrac{2}{20}}={\dfrac{1}{10}}. \]
  2. 求这 $ 3 $ 点与原点 $ O $ 共面的概率．
    标注
    答案
    略
    解析
    选取的这 $ 3 $ 个点与原点 $ O $ 共面的所有可能结果有：\[A_1A_2B_1,A_1A_2B_2,A_1A_2C_1,A_1A_2C_2,B_1B_2A_1,B_1B_2A_2,\\B_1B_2C_1,B_1B_2C_2,C_1C_2A_1,C_1C_2A_2,C_1C_2B_1,C_1C_2B_2\]共 $ 12 $ 种，因此，这 $ 3 $ 个点与原点 $ O $ 共面的概率为\[ P_2={\dfrac{12}{20}}={\dfrac{3}{5}}. \]
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.116074s